题目内容
已知集合A={y|y=x，x∈R}，B={y|y=x2，x∈R}则A∩B等于（ ）
| A、R |
| B、[0，+∞） |
| C、{（0，0），（1，1）} |
| D、∅ |
考点：交集及其运算
专题：集合
分析：由一次、二次函数的值域求出集合A、B，由交集的运算求出A∩B．
解答：
解：因为A={y|y=x，x∈R}=R，B={y|y=x2，x∈R}=[0，+∞），
所以A∩B=[0，+∞），
故选：B．
所以A∩B=[0，+∞），
故选：B．
点评：本题考查交集及其运算，以及一次、二次函数的值域，属于基础题．
练习册系列答案
名校课堂系列答案
相关题目
已知函数f（x）=x+
+m（p≠0）是奇函数，
（1）求m的值；
（2）若p=-1，用定义证明函数f（x）=x-
在区间（0，+∞）上的单调性．
（3）若p＜0，当x∈[1，3]时，求f（x）的最值．
| p |
| x |
（1）求m的值；
（2）若p=-1，用定义证明函数f（x）=x-
| 1 |
| x |
（3）若p＜0，当x∈[1，3]时，求f（x）的最值．
若集合A={x|
≤0}，B={x|x≥-2}且A⊆B．则实数a的取值范围是（ ）
| x-a |
| x-2 |
| A、（-∞，-2] |
| B、[-2，2] |
| C、[-2，+∞） |
| D、[2，+∞） |
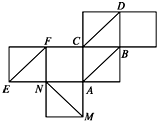如图为棱长是1的正方体的表面展开图，在原正方体中，给出下列三个命题：