题目内容
5.设函数f(x)=|x2-2x-1|,若m>n>1,且f(m)=f(n),则mn的取值范围为( )| A. | $({3,3+2\sqrt{2}})$ | B. | $({3,3+2\sqrt{2}}]$ | C. | (1,3) | D. | (1,3] |
分析 作出f(x)的图象,判断m,n的范围,根据f(m)=f(n)和基本不等式得出答案
解答 解:解方程x2-2x-1=0得x=1±$\sqrt{2}$,
∴当1-$\sqrt{2}$<x<1+$\sqrt{2}$时,x2-2x-1<0,
当x<1-$\sqrt{2}$或x>1+$\sqrt{2}$时,x2-2x-1>0,
作出f(x)的函数图象如图所示: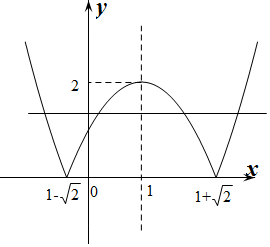
∵m>n>1,且f(m)=f(n),
∴1<n<1$+\sqrt{2}$,1+$\sqrt{2}$<m<3.
f(n)=-n2+2n+1,f(m)=m2-2m-1,
∵f(m)=f(n),
∴m2-2m-1+n2-2n-1=0,即(m+n-1)2=2mn+3,
∵m+n>2$\sqrt{mn}$>1,
∴(m+n-1)2>(2$\sqrt{mn}$-1)2=4mn-4$\sqrt{mn}$+1,
∴2mn+3>4mn-4$\sqrt{mn}$+1,解得0<$\sqrt{mn}$<1+$\sqrt{2}$,
∴mn<3+2$\sqrt{2}$,
故选:A.
点评 题考查了二次函数的性质,基本不等式的应用,属于中档题.

练习册系列答案
相关题目
1.已知集合A={x|x2-2x<0},B={x|y=log2(x-1)},则A∪B=( )
| A. | (0,+∞) | B. | (1,2) | C. | (2,+∞) | D. | (-∞,0) |
16.已知抛物线C:y2=8x的焦点为F,过F的直线l与抛物线C交于M(x1,y1),N(x2,y2)两点,若|MN|=8,则( )
| A. | x1+x2=8 | B. | x1+x2=4 | C. | y1+y2=8 | D. | y1+y2=4 |
13.三棱柱ABC-A1B1C1的侧棱与底面垂直,AA1=AB=AC=1,AB⊥AC,N是BC的中点,点P在A1B1上,且满足|A1P|=λ|A1B1|,直线PN与平面ABC所成角θ的正切值取最大值时λ的值为( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{2\sqrt{5}}{5}$ |
20.已知函数f(x)=$\left\{\begin{array}{l}{-(x+1)•{e}^{x},x≤a}\\{bx-1,x>a}\end{array}\right.$,若函数f(x)有最大值M,则M的取值范围是( )
| A. | ($-\frac{1}{2}-\frac{1}{2{e}^{2}}$,0) | B. | (0,$\frac{1}{{e}^{2}}$] | C. | (0,$\frac{1}{2}+\frac{1}{2{e}^{2}}$] | D. | ($\frac{1}{2{e}^{2}}-\frac{1}{2}$,$\frac{1}{{e}^{2}}$] |
10.已知y=f(x)是定义在R上的奇函数,且当x>0时,f(x)=2x-1,则f(-2)等于( )
| A. | 3 | B. | -3 | C. | -$\frac{3}{4}$ | D. | -$\frac{11}{4}$ |
14.已知变量x,y满足约束条件$\left\{\begin{array}{l}{x-y≤2}\\{x+y≤4}\\{x≥1}\end{array}\right.$,则x2+y2取值范围为( )
| A. | [1,8] | B. | [4,8] | C. | [1,10] | D. | [1,16] |