题目内容
10.已知y=f(x)是定义在R上的奇函数,且当x>0时,f(x)=2x-1,则f(-2)等于( )| A. | 3 | B. | -3 | C. | -$\frac{3}{4}$ | D. | -$\frac{11}{4}$ |
分析 根据题意,由函数的解析式计算可得f(2)的值,又由函数为奇函数,可得f(-2)=-f(2),即可得答案.
解答 解:根据题意,当x>0时,f(x)=2x-1,则f(2)=22-1=3,
又由函数f(x)为R上的奇函数,
则f(-2)=-f(2)=-3;
故选:B.
点评 本题考查函数的奇偶性的性质,关键是灵活运用函数的奇偶性的性质.

练习册系列答案
相关题目
18.在△ABC中,$|{\overrightarrow{AB}+\overrightarrow{AC}}|=\sqrt{3}|{\overrightarrow{AB}-\overrightarrow{AC}}|$,$|{\overrightarrow{AB}}|=|{\overrightarrow{AC}}|=3$,则$\overrightarrow{CB}•\overrightarrow{CA}$的值为( )
| A. | 3 | B. | -3 | C. | $-\frac{9}{2}$ | D. | $\frac{9}{2}$ |
5.设函数f(x)=|x2-2x-1|,若m>n>1,且f(m)=f(n),则mn的取值范围为( )
| A. | $({3,3+2\sqrt{2}})$ | B. | $({3,3+2\sqrt{2}}]$ | C. | (1,3) | D. | (1,3] |
20.D为△ABC的边BC的中点,E为AD中点,若AD=a,则($\overrightarrow{EB}$+$\overrightarrow{EC}$)•$\overrightarrow{EA}$=( )
| A. | -$\frac{{a}^{2}}{2}$ | B. | $\frac{{a}^{2}}{2}$ | C. | -2a2 | D. | a2 |
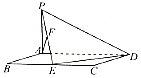 如图,平行四边形ABCD中,BC=2AB=4,∠ABC=60°,PA⊥AD,E,F分别为BC,PE的中点,AF⊥平面PED.
如图,平行四边形ABCD中,BC=2AB=4,∠ABC=60°,PA⊥AD,E,F分别为BC,PE的中点,AF⊥平面PED.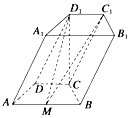 如图,在四棱柱ABCD-A1B1C1D1中,底面ABCD是等腰梯形,∠ADC=120°,AB=2CD=2,平面D1DCC1垂直平面ABCD,D1C⊥AB,M是线段AB的中点.
如图,在四棱柱ABCD-A1B1C1D1中,底面ABCD是等腰梯形,∠ADC=120°,AB=2CD=2,平面D1DCC1垂直平面ABCD,D1C⊥AB,M是线段AB的中点.