三棱柱ABC-A1B1C1的侧棱与底面垂直.AA1=AB=AC=1.AB⊥AC.N是BC的中点.点P在A1B1上.且满足|A1P|=λ|A1B1|.直线PN与平面ABC所成角θ的正切值取最大值时λ的值为( )A．$\frac{1}{2}$B．$\frac{\sqrt{2}}{2}$C．$\frac{\sqrt{3}}{2}$D．$\frac{2\sqrt{5}}{5}$ 题目和参考答案——青夏教育精英家教网—

题目内容

13．三棱柱ABC-A₁B₁C₁的侧棱与底面垂直，AA₁=AB=AC=1，AB⊥AC，N是BC的中点，点P在A₁B₁上，且满足|A₁P|=λ|A₁B₁|，直线PN与平面ABC所成角θ的正切值取最大值时λ的值为（　　）

A．

$\frac{1}{2}$

B．

$\frac{\sqrt{2}}{2}$

C．

$\frac{\sqrt{3}}{2}$

D．

$\frac{2\sqrt{5}}{5}$

分析过P作PM⊥AB于M，连接MN，则$tanθ=\frac{PM}{MN}=\frac{1}{MN}$，然后求解即可．

解答解：过P作PM⊥AB于M，连接MN，则$tanθ=\frac{PM}{MN}=\frac{1}{MN}$，
故当MN最小时tanθ最大．此时MN⊥AB，M为AB中点，∴$λ=\frac{1}{2}$．
故选：A．

点评本题考查直线与平面所成角的求法，考查空间想象能力以及计算能力．

练习册系列答案

4．设数列{a_n}满足a₁=$\frac{1}{3}$，a_n+1=a_n+$\frac{{a}_{n}^{2}}{{n}^{2}}$，n∈N，^*
（1）求a₂，a₃；
（2）证明：数列{a_n}为递增数列
（3）证明：$\frac{n}{2n+1}$≤a_n$≤\frac{2n-1}{2n+1}$，n∈N^*．

1．已知点P为一动点，点A的坐标为（1，$\frac{3}{2}$），点B的坐标为（1，-$\frac{3}{2}$）．两条不同的直线PA、PB与x轴交点的横坐标分别为m、n且满足mn=4，记动点P的轨迹及A，B两点组成曲线C，设过点（0，1）且斜率为k的直线l与曲线C交于不同的两点M，N，线段MN的中点为E点，直线OE与曲线C交于Q、R两点．
（1）求曲线C的方程；
（2）若|EM|•|EN|=λ|EQ|•|ER|，求实数λ的取值范围．

8．

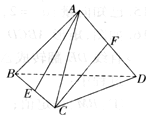如图，正四面体ABCD中，E、F分别是棱BC和AD的中点，则直线AE和CF所成的角的余弦值为（　　）

18．在△ABC中，$|{\overrightarrow{AB}+\overrightarrow{AC}}|=\sqrt{3}|{\overrightarrow{AB}-\overrightarrow{AC}}|$，$|{\overrightarrow{AB}}|=|{\overrightarrow{AC}}|=3$，则$\overrightarrow{CB}•\overrightarrow{CA}$的值为（　　）

5．设函数f（x）=|x²-2x-1|，若m＞n＞1，且f（m）=f（n），则mn的取值范围为（　　）

2．设数列{a_n}是等差数列，数列{b_n}的前n项和S_n满足S_n=2（b_n-1），且a₂=b₁-1，a₅=b₃-1．
（Ⅰ）求数列{a_n}和{b_n}的通项公式；
（Ⅱ）设c_n=a_n•b_n，求数列{c_n}的前n项和T_n．

3．已知数列{a_n}的前n项和为S_n，且满足a₁=1，a_n•a_n+1=2S_n，设b_n=$\frac{{a}_{n}}{{3}^{{a}_{n}}}$，若存在正整数p，q（p＜q），使得b₁，b_p，b_q成等差数列，则p+q=5．

试题分类