题目内容
已知f(x)、g(x)都是定义在R上的函数,g(x)≠0,f′(x)g(x)-f(x)g′(x)<0,
=ax,
+
=
,则关于x的方程abx2+
x+
=0(b∈(0,1))有两个不同实根的概率为( )
| f(x) |
| g(x) |
| f(1) |
| g(1) |
| f(-1) |
| g(-1) |
| 5 |
| 2 |
| 2 |
| 5 |
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:几何概型
专题:概率与统计
分析:根据函数的单调性和导数之间的关系求出a的值,然后利用几何概型的概率公式即可得到结论.
解答:
解:∵f(x)=axg(x),
∴
=ax,
∵f′(x)g(x)-f(x)g′(x)<0
∴[
]′=
<0,
即函数
=ax,单调递减,即0<a<1.
又
+
=
,
则a+
=
,解得a=
.
∵关于x的方程abx2+
x+
=0(b∈(0,1))有两个不同实根,
∴△=2-10ab>0,即0<b<
,
∴根据几何概型的概率公式可知所求的概率P=
=
,
故选:B
∴
| f(x) |
| g(x) |
∵f′(x)g(x)-f(x)g′(x)<0
∴[
| f(x) |
| g(x) |
| f′(x)g(x)-f(x)g′(x) |
| g2(x) |
即函数
| f(x) |
| g(x) |
又
| f(1) |
| g(1) |
| f(-1) |
| g(-1) |
| 5 |
| 2 |
则a+
| 1 |
| a |
| 5 |
| 2 |
| 1 |
| 2 |
∵关于x的方程abx2+
| 2 |
| 5 |
| 2 |
∴△=2-10ab>0,即0<b<
| 2 |
| 5 |
∴根据几何概型的概率公式可知所求的概率P=
| ||
| 1-0 |
| 2 |
| 5 |
故选:B
点评:本题主要考查几何概型的概率的计算,利用导数研究函数的单调性,求出a的值是解决本题的关键.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
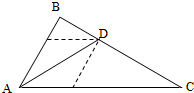 如图,△ABC中,∠A=60°,∠A的平分线交BC于D,若AB=4,且
如图,△ABC中,∠A=60°,∠A的平分线交BC于D,若AB=4,且| AD |
| 1 |
| 4 |
| AC |
| AB |
A、2
| ||
B、3
| ||
C、4
| ||
D、5
|
已知变量x,y满足约束条件
,若目标函数z=y+ax仅在点(5,3)处取得最小值,则实数a的取值范围为( )
|
| A、(-∞,-1) | ||
| B、(0,+∞) | ||
C、(
| ||
| D、(1,+∞) |
已知函数f(x)的定义域为(-∞,+∞),如果f(x+2014)=
那么f(2014+
)•f(-7986)=( )
|
| π |
| 4 |
| A、2014 | ||
| B、4 | ||
C、
| ||
D、
|
任取实数a、b∈[-1,1],则a、b满足|a-2b|≤2的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
设p:“a>3”q:“f(x)=x3-ax2+1在(0,2)上有唯一零点”,则p是q的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |