题目内容
已知函数f(x)的定义域为(-∞,+∞),如果f(x+2014)=
那么f(2014+
)•f(-7986)=( )
|
| π |
| 4 |
| A、2014 | ||
| B、4 | ||
C、
| ||
D、
|
考点:函数的值
专题:函数的性质及应用
分析:根据函数的表达式分别进行计算即可得到结论.
解答:
解:由函数的表达式可知f(2014+
)=
sin
=
×
=1,
f(-7986)=f(-10000+2014)=lg(10000)=4,
∴f(2014+
)•f(-7986)=4,
故选:B.
| π |
| 4 |
| 2 |
| π |
| 4 |
| 2 |
| ||
| 2 |
f(-7986)=f(-10000+2014)=lg(10000)=4,
∴f(2014+
| π |
| 4 |
故选:B.
点评:本题注意考查函数值的计算,根据分段函数的表达式直接代入是解决本题的关键,比较基础.

练习册系列答案
相关题目
已知f(x)、g(x)都是定义在R上的函数,g(x)≠0,f′(x)g(x)-f(x)g′(x)<0,
=ax,
+
=
,则关于x的方程abx2+
x+
=0(b∈(0,1))有两个不同实根的概率为( )
| f(x) |
| g(x) |
| f(1) |
| g(1) |
| f(-1) |
| g(-1) |
| 5 |
| 2 |
| 2 |
| 5 |
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知某几何体的三视图(单位:cm)如图所示,则该几何体的体积是( )


| A、48cm3 |
| B、98cm3 |
| C、98cm3 |
| D、78cm3 |
某三棱锥的三视图如图所示,该三棱锥的体积是( )


A、18
| ||
B、36
| ||
C、12
| ||
D、24
|
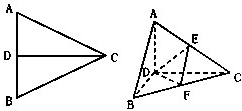 CD是正△ABC的边AB上的高,E,F分别是AC和BC边的中点,现将△ABC沿CD翻折成直二面角A-DC-B,如图所示.
CD是正△ABC的边AB上的高,E,F分别是AC和BC边的中点,现将△ABC沿CD翻折成直二面角A-DC-B,如图所示. 如图,设椭圆C:
如图,设椭圆C: