题目内容
已知不等式ax2-3x+2<0的解集为A={x|1<x<b}
(1)求a,b的值;
(2)求函数f(x)=(2a+b)x-
在区间[3,5]上的最小值.
(1)求a,b的值;
(2)求函数f(x)=(2a+b)x-
| 9 |
| (a-b)x |
考点:一元二次不等式的解法
专题:不等式的解法及应用
分析:(1)利用一元二次不等式的解集与相应的一元二次方程的实数根的关系即可求出;
(2)求出函数f(x)在区间[3,5]上的单调性,最值即可求出.
(2)求出函数f(x)在区间[3,5]上的单调性,最值即可求出.
解答:
解:(1)∵不等式ax2-3x+2<0的解集为A={x|1<x<b},
∴方程ax2-3x+2=0的解为1,b,且b>1.
∴
解得a=1,b=2,
(2)由(1)知,f(x)=4x+
,
∴f′(x)=4-
=
当x>
或x<-
时,f′(x)>0,即f(x)为单调递增函数,
∴f(x)在区间[3,5]上为增函数,
∴当x=3时,f(x)有最小值,最小值为f(3)=15.
∴方程ax2-3x+2=0的解为1,b,且b>1.
∴
|
解得a=1,b=2,
(2)由(1)知,f(x)=4x+
| 9 |
| x |
∴f′(x)=4-
| 9 |
| x2 |
| 4x2-9 |
| x2 |
当x>
| 3 |
| 2 |
| 3 |
| 2 |
∴f(x)在区间[3,5]上为增函数,
∴当x=3时,f(x)有最小值,最小值为f(3)=15.
点评:熟练掌握一元二次不等式的解集与相应的一元二次方程的实数根的关系和利用导数判断单调性是解题的关键.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
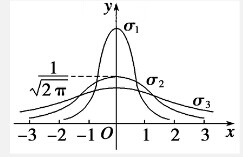 如图,当σ取三个不同的值σ1,σ2,σ3的三种正态曲线N(0,σ2)的图象,那么σ1,σ2,σ3的大小关系是( )
如图,当σ取三个不同的值σ1,σ2,σ3的三种正态曲线N(0,σ2)的图象,那么σ1,σ2,σ3的大小关系是( )| A、σ1>1>σ2>σ3>0 |
| B、0<σ1<σ2<1<σ3 |
| C、σ1>σ2>1>σ3>0 |
| D、0<σ1<σ2=1<σ3 |
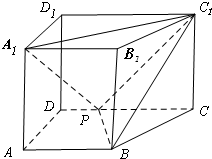 如图,直四棱柱ABCD-A1B1C1D1底面ABCD直角梯形,AB∥CD,∠BAD=90°,P是棱CD上一点,AB=2,AD=
如图,直四棱柱ABCD-A1B1C1D1底面ABCD直角梯形,AB∥CD,∠BAD=90°,P是棱CD上一点,AB=2,AD=