题目内容
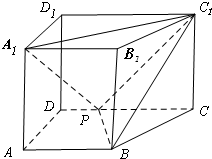 如图,直四棱柱ABCD-A1B1C1D1底面ABCD直角梯形,AB∥CD,∠BAD=90°,P是棱CD上一点,AB=2,AD=
如图,直四棱柱ABCD-A1B1C1D1底面ABCD直角梯形,AB∥CD,∠BAD=90°,P是棱CD上一点,AB=2,AD=| 2 |
(1)求直四棱柱ABCD-A1B1C1D1的侧面积和体积;
(2)求证:PB⊥平面BCC1B1.
考点:直线与平面垂直的判定,棱柱、棱锥、棱台的体积
专题:空间位置关系与距离
分析:(1)先通过梯形面积公式求得底面的面积,最后利用体积公式求得四棱锥的体积;过B作BM⊥CD交CD于M,分别求得BM,MC和BC,最后求得四个侧面的面积相加即可求得棱锥的侧面积.
(2)先分别求得PC1,BC1和PB利用勾股定理证明出PB⊥BC1,然后根据线面垂直的性质证明出B1B⊥PB.最后根据线面垂直的判定定理证明出PB⊥平面BCC1B1.
(2)先分别求得PC1,BC1和PB利用勾股定理证明出PB⊥BC1,然后根据线面垂直的性质证明出B1B⊥PB.最后根据线面垂直的判定定理证明出PB⊥平面BCC1B1.
解答:
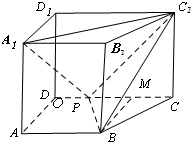 解:(1)底面直角梯形的面积S=
解:(1)底面直角梯形的面积S=
(AB+CD)•AD=3
,V=S•AA1=9
,
过B作BM⊥CD交CD于M,在Rt△BMC中,BM=
,MC=2,则BC=
,
侧面积S侧=(
+2+
+4)×3=18+3
+3
.
(2)∵PC1=
=3
,BC1=
=
,PB=
=
∴P
=PB2+B
,
∴PB⊥BC1,
∵B1B⊥平面ABCD,
∴B1B⊥PB.
又B1B∩BC=B,
∴PB⊥平面BCC1B1.
 解:(1)底面直角梯形的面积S=
解:(1)底面直角梯形的面积S=| 1 |
| 2 |
| 2 |
| 2 |
过B作BM⊥CD交CD于M,在Rt△BMC中,BM=
| 2 |
| 6 |
侧面积S侧=(
| 2 |
| 6 |
| 2 |
| 6 |
(2)∵PC1=
| 32+32 |
| 2 |
| 6-32 |
| 15 |
| 2+1 |
| 3 |
∴P
| C | 2 1 |
| C | 2 1 |
∴PB⊥BC1,
∵B1B⊥平面ABCD,
∴B1B⊥PB.
又B1B∩BC=B,
∴PB⊥平面BCC1B1.
点评:本题主要考查了线面垂直的判定定理的应用以及几何体的体积的运算.考查了学生空间观察能力和运算能力.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
函数f(x)=Asin(ωx+φ)(A>0,|φ|<
)的图象相邻两个对称中心间距离为π,且f(x)有一条对称轴是x=
,则函数y=f(
-x)是( )
| π |
| 2 |
| π |
| 4 |
| π |
| 4 |
| A、偶函数且在x=0处取最小值 |
| B、偶函数且在x=0处取最大值 |
| C、奇函数且在x=0处取最大值 |
| D、奇函数且在x=0处取最小值 |