题目内容

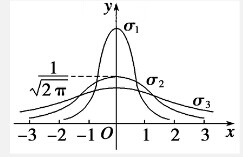如图，当σ取三个不同的值σ1，σ2，σ3的三种正态曲线N（0，σ2）的图象，那么σ1，σ2，σ3的大小关系是（　　）
A、σ1＞1＞σ2＞σ3＞0
B、0＜σ1＜σ2＜1＜σ3
C、σ1＞σ2＞1＞σ3＞0
D、0＜σ1＜σ2=1＜σ3
考点：正态分布曲线的特点及曲线所表示的意义
专题：规律型,概率与统计
分析：由正态分布曲线的特点及曲线所表示的意义，可得结论．
解答： 解：由正态分布曲线的特点及曲线所表示的意义，可知：
当0＜σ＜1时，它与y轴交点的纵坐标大于f（0）=
1
2πσ
；
当σ＞1时，它与y轴交点的纵坐标小于f（0）．结合图象可知选D．
故选：D．
点评：本题考查正态曲线的性质，比较基础．
练习册系列答案
相关题目
双曲线的
x2
a2
-
y2
4
=1（a＞0）的一条渐近线方程是y=
2
3
x，则a=（　　）
A、
3
B、3
C、6
D、9
2sin
π
12
cos
π
12
的值是（　　）
A、
1
8
B、
1
4
C、
1
2
D、1
若抛物线C1：y2=4x的焦点F恰好是双曲线C2：
x2
a2
-
y2
b2
=1（a＞0，b＞0）的右焦点，且C1与C2交点的连线过点F，则双曲线C2的离心率为（　　）
A、
2
+1
B、2
2
-1
C、3+2
2
D、
6
+
2
2
函数f（x）=Asin（ωx+φ）（A＞0，|φ|＜
π
2
）的图象相邻两个对称中心间距离为π，且f（x）有一条对称轴是x=
π
4
，则函数y=f（
π
4
-x）是（　　）
A、偶函数且在x=0处取最小值
B、偶函数且在x=0处取最大值
C、奇函数且在x=0处取最大值
D、奇函数且在x=0处取最小值
已知数列{an}的前n项和为Sn，且Sn=n2-8n，令bn=|an|．
（1）求数列{an}的通项公式；
（2）求数列{bn}的前n项和Tn的表达式．
已知抛物线方程为x2=4y，过点M（0，2）作直线与抛物线交于两点A（x1，y1），B（x2，y2），过A，B分别作抛物线的切线，两切线的交点为P．
（Ⅰ）求x1x2的值；
（Ⅱ）求点P的纵坐标；
（Ⅲ）求△PAB面积的最小值．
已知函数f（x）=ax+
b
x
+c（a＞0）的图象在点（1，f（1））处的切线方程为y=x-1．
（1）用a表示出b，c；
（2）证明：当a≥
1
2
时，f（x）≥1nx在[1，+∞）上恒成立；
（3）证明：1+
1
2
+
1
3
+…+
1
n
＞1n（n+1）+
n
2(n+1)
．（n∈N*）
已知不等式ax2-3x+2＜0的解集为A={x|1＜x＜b}
（1）求a，b的值；
（2）求函数f（x）=（2a+b）x-
9
(a-b)x
在区间[3，5]上的最小值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网