题目内容
8.已知直线l过点(3,2),且与两条坐标轴围成一个等腰直角三角形,则直线l的方程为x-y-1=0或x+y-5=0.分析 设直线方程为$\frac{x}{a}$+$\frac{y}{a}$=1或$\frac{x}{a}$-$\frac{y}{a}$=1,把点(3,2)代入直线方程解a可得.
解答 解:由题意设直线方程为$\frac{x}{a}$+$\frac{y}{a}$=1或$\frac{x}{a}$-$\frac{y}{a}$=1,把点(3,2)代入直线方程得$\frac{3}{a}$+$\frac{2}{a}$=1或得$\frac{3}{a}$-$\frac{2}{a}$=1
解得a=1,或a=5,
所以所求的直线为:x-y-1=0或x+y-5=0
故答案为:x-y-1=0或x+y-5=0.
点评 本题考查用截距式求直线的方程,体现了分类讨论的数学思想,设出直线方程是解决问题的关键,属基础题.

练习册系列答案
相关题目
13.已知命题p:?x∈(0,+∞),3x-cosx>0,则下列叙述正确的是( )
| A. | ¬p:?x∈(0,+∞),3x-cosx≤0 | B. | ¬p:?x∈(0,+∞),3x-cosx<0 | ||
| C. | ¬p:?x∈(-∞,0],3x-cosx≤0 | D. | ¬p是假命题 |
20.以下关于函数f(x)=sin2x-cos2x的命题,正确的是( )
| A. | 函数f(x)在区间$(0,\frac{2}{3}π)$上单调递增 | |
| B. | 直线$x=\frac{π}{8}$是函数y=f(x)图象的一条对称轴 | |
| C. | 点$(\frac{π}{4},0)$是函数y=f(x)图象的一个对称中心 | |
| D. | 将函数y=f(x)的图象向左平移$\frac{π}{8}$个单位,可得到$y=\sqrt{2}sin2x$的图象 |
17.三次函数$f(x)=a{x^3}-\frac{3}{2}{x^2}+2x+1$的图象在点(1,f(1))处的切线与x轴平行,则f(x)在区间(1,3)上的最小值是( )
| A. | $\frac{8}{3}$ | B. | $\frac{11}{6}$ | C. | $\frac{11}{3}$ | D. | $\frac{5}{3}$ |
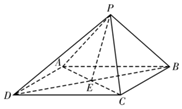 如图,四棱锥P-ABCD的底面ABCD是菱形,∠ADC=60°,PA=PC,PD⊥PB,AC∩BD=E,二面角P-AC-B的大小为60°.
如图,四棱锥P-ABCD的底面ABCD是菱形,∠ADC=60°,PA=PC,PD⊥PB,AC∩BD=E,二面角P-AC-B的大小为60°.
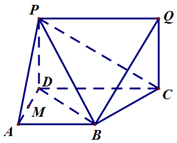 如图,在直角梯形ABCD中,AB⊥AD,AB∥CD,PD⊥面ABCD,QC⊥面ABCD,且AB=AD=PD=QC=$\frac{1}{2}$CD,
如图,在直角梯形ABCD中,AB⊥AD,AB∥CD,PD⊥面ABCD,QC⊥面ABCD,且AB=AD=PD=QC=$\frac{1}{2}$CD,