题目内容
18.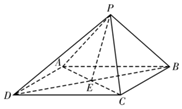 如图,四棱锥P-ABCD的底面ABCD是菱形,∠ADC=60°,PA=PC,PD⊥PB,AC∩BD=E,二面角P-AC-B的大小为60°.
如图,四棱锥P-ABCD的底面ABCD是菱形,∠ADC=60°,PA=PC,PD⊥PB,AC∩BD=E,二面角P-AC-B的大小为60°.(1)证明:AC⊥PB;
(2)求二面角E-PD-C的余弦值.
分析 (1)推导出AC⊥PE,AC⊥BD,由此能证明AC⊥PB.
(2)推导出CE⊥PD,过E作EH⊥PD于H,连接CH,则PD⊥面CEH,∠CHE是二面角E-PD-C的平面角.由此能求出二面角E-PD-C的余弦值.
解答 证明:(1)∵E是AC的中点,PA=PC,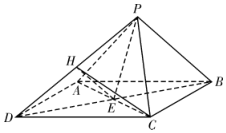
∴AC⊥PE,
∵底面ABCD是菱形,∴AC⊥BD,
又PE∩BD=E,∴AC⊥面PDB,
又PB?面PDB,∴AC⊥PB.
解:(2)由(1)CE⊥面PDB,PD?面PDB,∴CE⊥PD,
过E作EH⊥PD于H,连接CH,则PD⊥面CEH,
又CH?面CEH,则PD⊥CH,
∴∠CHE是二面角E-PD-C的平面角.
由(1)知∠PEB是二面角P-AC-B的平面角,所以∠PEB=60°,
设AB=a,在Rt△PDB中,$PE=\frac{1}{2}BD=BE=\frac{{\sqrt{3}}}{2}a$,△PBE是等边三角形,$PB=\frac{{\sqrt{3}}}{2}a$,EH是△PBD的中位线,
则$EH=\frac{1}{2}PB=\frac{{\sqrt{3}}}{4}a$,$CE=\frac{a}{2}$,CH=$\sqrt{C{E}^{2}+E{H}^{2}}$=$\frac{\sqrt{7}}{4}a$,
∴$cos∠CHE=\frac{EH}{CH}=\frac{{\sqrt{21}}}{7}$,
即二面角E-PD-C的余弦值为$\frac{{\sqrt{21}}}{7}$.
点评 本题考查线线垂直的证明,考查二面角的余弦值的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 小题狂做系列答案
小题狂做系列答案
相关题目
6.函数$y=\sqrt{{{log}_2}(x-3)}$的定义域是( )
| A. | (3,+∞) | B. | (3,4] | C. | (4,+∞) | D. | [4,+∞) |
3.设F1,F2是椭圆$\frac{x^2}{a^2}+\frac{y^2}{25}=1(a<5)$的两个焦点,且|F1F2|=8,弦AB过点F2,则△ABF1的周长为( )
| A. | 12 | B. | 20 | C. | 2$\sqrt{41}$ | D. | 4$\sqrt{41}$ |
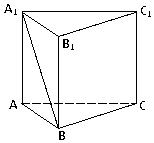 如图,在直三棱柱ABC-A1B1C1中,AB=2,AC=AA1=4,∠ABC=90°;
如图,在直三棱柱ABC-A1B1C1中,AB=2,AC=AA1=4,∠ABC=90°;