题目内容
7.(1)把圆锥曲线C的参数方程:$\left\{\begin{array}{l}x={t^2}+\frac{1}{t^2}-2\\ y=t-\frac{1}{t}\end{array}\right.(t$为参数)化为直角坐标方程;(2)若两条曲线的极坐标方程分别为ρ=1与ρ=2cos(θ+$\frac{π}{3}$),它们相交于A、B两点,求线段AB的长.
分析 (1)消去参数,可得直角坐标方程;
(2)先将原极坐标方程化成直角坐标方程,再利用直角坐标方程进行判断.
解答 解:(1)圆锥曲线C的参数方程:$\left\{\begin{array}{l}x={t^2}+\frac{1}{t^2}-2\\ y=t-\frac{1}{t}\end{array}\right.(t$为参数),可得y2=t2+$\frac{1}{{t}^{2}}$-2=x;
(2)由ρ=1得x2+y2=1,
又∵ρ=2cos(θ+$\frac{π}{3}$)=cosθ-$\sqrt{3}$sinθ,
∴ρ2=ρcosθ-$\sqrt{3}ρ$sinθ,
∴x2+y2-x+$\sqrt{3}$y=0,
联立两方程,解得A(1,0),B(-$\frac{1}{2}$,-$\frac{\sqrt{3}}{2}$),
∴|AB|=$\sqrt{(1+\frac{1}{2})^{2}+(\frac{\sqrt{3}}{2})^{2}}$=$\sqrt{3}$.
点评 本题考查参数方程与普通方程的互化,考查点的极坐标和直角坐标的互化,利用直角坐标与极坐标间的关系,即利用ρcosθ=x,ρsinθ=y,ρ2=x2+y2,进行代换即得.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
15.已知集合A={x|(x+1)(x-2)<0},非空集合B={x|2a<x<6},则“A∩B=∅”的充分不必要条件可以是( )
| A. | -1<a<2 | B. | 1≤a<3 | C. | a>0 | D. | 1<a<3 |
2.已知随机变量ε的分布列如下表:
求其数学期望、方差和标准差.
| ε | 0 | 1 | 2 | 3 | 4 |
| p | 0.2 | 0.4 | 0.3 | 0.08 | 0.02 |
12.已知函数y=f(x)上任一点(x0,f(x0))处的切线斜率$k=({{x_0}-2}){({{x_0}+1})^2}$,则该函数的单调递减区间为( )
| A. | [-1,+∞) | B. | (-∞,2] | C. | (-∞,-1),(1,2) | D. | [2,+∞) |
16.集合A={-1,1},B={x|mx=1},A∪B=A,则实数m组成的集合( )
| A. | {-1} | B. | {1} | C. | {-1,1} | D. | {-1,0,1} |
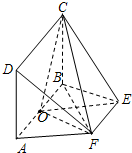 如图,AB为圆O的直径,点E、F在圆O上,矩形ABCD所在的平面和圆O所在的平面互相垂直,且AB=2,AD=EF=1.
如图,AB为圆O的直径,点E、F在圆O上,矩形ABCD所在的平面和圆O所在的平面互相垂直,且AB=2,AD=EF=1.