题目内容
17.三次函数$f(x)=a{x^3}-\frac{3}{2}{x^2}+2x+1$的图象在点(1,f(1))处的切线与x轴平行,则f(x)在区间(1,3)上的最小值是( )| A. | $\frac{8}{3}$ | B. | $\frac{11}{6}$ | C. | $\frac{11}{3}$ | D. | $\frac{5}{3}$ |
分析 求出函数的导数,求得切线的斜率,由两直线平行的条件:斜率相等,解方程可得a,再求f(x)在区间(1,3)上的最小值.
解答 解:f′(x)=3ax2-3x+2,
由图象在(1,f(1))处的切线平行于x轴,
可得f′(1)=3a-3+2=0,
解得a=$\frac{1}{3}$,
∴f′(x)=(x-1)(x-2),
函数在(1,2)上单调递减,(2,3)上单调递增,
∴x=2时,f(x)在区间(1,3)上的最小值是$\frac{5}{3}$.
故选D.
点评 本题考查导数的运用:求切线的斜率,函数的单调性与最值,考查导数的几何意义:函数在某点处的导数即为曲线在该点处的切线的斜率,考查运算能力,属于中档题.

练习册系列答案
相关题目
5.某工厂第三年的产量比第一年的产量增加20%,若每年的平均增长率相同(设为x),则以下结论正确的是( )
| A. | x=10% | B. | x<10% | ||
| C. | x>10% | D. | x的大小由第一年的产量决定 |
12.一个几何体的三视图如图所示,则此几何体的表面积为( )
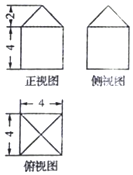

| A. | $80+16\sqrt{2}$ | B. | $96+13\sqrt{2}$ | C. | 96 | D. | 112 |
15.已知集合A={x|(x+1)(x-2)<0},非空集合B={x|2a<x<6},则“A∩B=∅”的充分不必要条件可以是( )
| A. | -1<a<2 | B. | 1≤a<3 | C. | a>0 | D. | 1<a<3 |
16.集合A={-1,1},B={x|mx=1},A∪B=A,则实数m组成的集合( )
| A. | {-1} | B. | {1} | C. | {-1,1} | D. | {-1,0,1} |