题目内容
20.以下关于函数f(x)=sin2x-cos2x的命题,正确的是( )| A. | 函数f(x)在区间$(0,\frac{2}{3}π)$上单调递增 | |
| B. | 直线$x=\frac{π}{8}$是函数y=f(x)图象的一条对称轴 | |
| C. | 点$(\frac{π}{4},0)$是函数y=f(x)图象的一个对称中心 | |
| D. | 将函数y=f(x)的图象向左平移$\frac{π}{8}$个单位,可得到$y=\sqrt{2}sin2x$的图象 |
分析 利用两角和差的正弦公式化简函数的解析式,再利用正弦函数的图象和性质,得出结论.
解答 解:函数f(x)=sin2x-cos2x=$\sqrt{2}$sin(2x-$\frac{π}{4}$),在区间$(0,\frac{2}{3}π)$上,2x-$\frac{π}{4}$∈(-$\frac{π}{4}$,$\frac{13π}{12}$),故函数在区间$(0,\frac{2}{3}π)$上不单调,故排除A;
令x=$\frac{π}{8}$,求得f(x)=0,不是函数的最值,故直线$x=\frac{π}{8}$不是函数y=f(x)图象的一条对称轴,故排除B;
令x=$\frac{π}{4}$,求得f(x)=1≠0,故点$(\frac{π}{4},0)$不是函数y=f(x)图象的一个对称中心,故排除C;
将函数y=f(x)的图象向左平移$\frac{π}{8}$个单位,可得到 y=$\sqrt{2}$sin[2(x+$\frac{π}{8}$)-$\frac{π}{4}$═$\sqrt{2}$sin2x的图象,
故D正确.
故选:D.
点评 本题主要考查两角和差的正弦公式,正弦函数的图象和性质,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.在区间$[{-\frac{π}{4},\frac{2π}{3}}]$上任取一个数x,则函数$f(x)=3sin({2x-\frac{π}{6}})$的值不小于0的概率为( )
| A. | $\frac{3}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{6}{11}$ | D. | $\frac{7}{12}$ |
5.某工厂第三年的产量比第一年的产量增加20%,若每年的平均增长率相同(设为x),则以下结论正确的是( )
| A. | x=10% | B. | x<10% | ||
| C. | x>10% | D. | x的大小由第一年的产量决定 |
12.一个几何体的三视图如图所示,则此几何体的表面积为( )
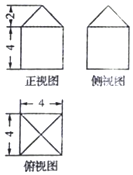

| A. | $80+16\sqrt{2}$ | B. | $96+13\sqrt{2}$ | C. | 96 | D. | 112 |
 已知函数f(x)=sin(2x+$\frac{π}{4}$)+1.
已知函数f(x)=sin(2x+$\frac{π}{4}$)+1.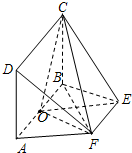 如图,AB为圆O的直径,点E、F在圆O上,矩形ABCD所在的平面和圆O所在的平面互相垂直,且AB=2,AD=EF=1.
如图,AB为圆O的直径,点E、F在圆O上,矩形ABCD所在的平面和圆O所在的平面互相垂直,且AB=2,AD=EF=1.