题目内容

已知向量
a
=（cosx，sinx），
b
=（-cosx，xosx），
c
=（-1，0）
（1）若x=
π
6
，求
a
，
c
的夹角；
（2）求函数f（x）=2
a
•
b
+1的单调递增区间．
考点：平面向量的综合题
专题：三角函数的图像与性质,平面向量及应用
分析：运用向量的运算求解，转换为求三角函数的图象和性质来解决．
解答： 解：（1）当x=
π
6
，
a
=（
3
2
，
1
2
），cos＜
a
，
c
＞=
a
•
c
|
a|
•|
c
|
=-
3
2
，
0≤＜
a
，
c
＞≤π，∴
a
与
c
的夹角为
5π
6

（2）函数f（x）=2
a
•
b
+1=2（-cos2x+sinxcosx）+1=2sinxcosx-（2cos2x-1）=sin2x-cos2x=
2
sin（2x-
π
4
）
当2kπ-
π
2
≤2x-
π
4
≤
π
2
+2kπ，k∈z，
即kπ-
π
8
≤x≤kπ+
π
8
，k∈z．
∴函数的单调递增区间为[kπ-
π
8
，kπ+
π
8
]k∈z．
点评：本题考察了平面向量的运算与三角函数图象性质的结合．
练习册系列答案
相关题目
已知sin（x+
π
6
）=
1
4
，x∈[
π
2
，π]，求sin2x的值．
已知
a
=（
3
cosx-
3
，sinx），
b
=（1+cosx，cosx），设f（x）=
a
•
b
，求：
（1）f（x）的解析式并简化；
（2）求函数f（x）在区间[0，
π
6
]上的值域．
已知椭圆E：
x2
a2
+
y2
b2
=1（a＞b＞0）的离心率e=
3
2
，并且经过定点P（
3
，
1
2
）．
（Ⅰ）求椭圆E的方程；
（Ⅱ）问是否存在直线y=-x+m，使直线与椭圆交于A、B两点，满足
OA
•
OB
=
12
5
，若存在求m值，若不存在说明理由．
已知直线l的方程为kx-y+1=0（k∈R），圆C的方程为x2+y2-2x-3=0．
（1）试判断直线与圆C的位置关系，并说明理由．
（2）过点（0，1）作直线l1⊥l，设直线l1与圆C相交于M，N两点，直线l与圆C相交于P，Q两点，则四边形PMQN的面积是否存在最大值和最小值？若存在，请求出，否则说明理由．
已知y=f（x）是定义在[-1，1]上的奇函数，x∈[0，1]时，f（x）=
4x+a
4x+1
．
（1）求x∈[-1，0）时，y=f（x）解析式；
（2）解不等式f（x）＞
1
5
．
当x＞1时，关于函数f（x）=x+
1
x-1
，则函数f（x）有最小值
 
．
已知定义在R上的偶函数f（x），当x≥0时，f（x）=x|x-2|．
（1）求y=f（x）的解析式．
（2）若函数y=a与函数y=f（x）有6个交点，求a的取值范围．
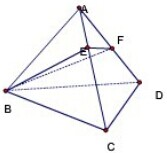正三棱锥A-BCD底面边长为a，侧棱长为2a，E、F分别为AC，AD上的动点，求截面△BEF周长的最小值和这时E、F的位置．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网