题目内容
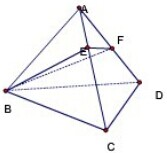正三棱锥A-BCD底面边长为a，侧棱长为2a，E、F分别为AC，AD上的动点，求截面△BEF周长的最小值和这时E、F的位置．考点：棱锥的结构特征
专题：空间位置关系与距离
分析：首先，展开三棱锥，然后，两点间的连接线BB'即是截面周长的最小值，然后，求解其距离即可．
解答：
解：把正三棱锥A-BCD的侧面展开，两点间的连接线BB'即是截面周长的最小值．
∵BB′∥CD，
∴△ADB′∽△B′FD，
∴DF/DB’=DB’/AD
其中AD=2a，DB’=a．
∴DF=
a
又△AEF∽△ACD，
∴EF/CD=AF/AD，其中CD=a，AD=2a，AF=2a-
a=
a，
∴EF=
a，
∴截面周长最小值是BB’=2a+
a=
a，E、F两点分别满足AE=AF=
a．
∵BB′∥CD，
∴△ADB′∽△B′FD，
∴DF/DB’=DB’/AD
其中AD=2a，DB’=a．
∴DF=
| 1 |
| 2 |
又△AEF∽△ACD，
∴EF/CD=AF/AD，其中CD=a，AD=2a，AF=2a-
| 1 |
| 2 |
| 3 |
| 2 |
∴EF=
| 3 |
| 4 |
∴截面周长最小值是BB’=2a+
| 3 |
| 4 |
| 11 |
| 4 |
| 3 |
| 2 |
点评：本题重点考查了空间中的距离最值问题，属于中档题．注意等价转化思想的灵活运用．
练习册系列答案
阅读快车系列答案
相关题目
一个正方形被分成九个相等的小正方形，将中间的一个正方形挖去，如图（1）；再将剩余的每个正方形都分成九个相等的小正方形，并将中间的一个挖去，得图（2）；如此继续下去，则第n个图共挖去小正方形（ ）| A、（8n-1）个 | ||
| B、（8n+1）个 | ||
C、
| ||
D、
|
已知如图，点A（-a，0），点B（a，0），l为圆x2+y2=a2的切线，P为切点，做AM⊥l交BP于M，则点M的轨迹方程为