题目内容
已知sin(x+
)=
,x∈[
,π],求sin2x的值.
| π |
| 6 |
| 1 |
| 4 |
| π |
| 2 |
考点:两角和与差的正弦函数,三角函数的化简求值
专题:计算题,三角函数的求值
分析:由x的范围,求得x+
的范围,求出cos(x+
),再由x=(x+
)-
,分别求出sinx,cosx,再由二倍角的正弦公式,即可得到所求值.
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
解答:
解:∵x∈[
,π],∴x+
∈[
,
],
∴cos(x+
)=-
=-
=-
,
∴cosx=cos[(x+
)-
]=cos(x+
)cos
+sin(x+
)sin
,
=(-
)×
+
×
=
,
sinx=sin[(x+
)-
]=sin(x+
)cos
-cos(x+
)sin
=
×
-(-
)×
=
,
∴sin2x=2sinxcosx=2×
×
=
.
| π |
| 2 |
| π |
| 6 |
| 2π |
| 3 |
| 7π |
| 6 |
∴cos(x+
| π |
| 6 |
1-sin2(x+
|
1-
|
| ||
| 4 |
∴cosx=cos[(x+
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
=(-
| ||
| 4 |
| ||
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
1-3
| ||
| 8 |
sinx=sin[(x+
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
=
| 1 |
| 4 |
| ||
| 2 |
| ||
| 4 |
| 1 |
| 2 |
| ||||
| 8 |
∴sin2x=2sinxcosx=2×
1-3
| ||
| 8 |
| ||||
| 8 |
=
-
| ||||
| 16 |
点评:本题考查三角函数的求值,考查角的变换,以及两角和差的正弦、余弦公式,二倍角公式,考查学生的计算能力,属于中档题和易错题.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
函数y=
的定义域为( )
| log2(2x2-x) |
A、{x|x≤-
| ||
B、{x|x<-
| ||
C、{x|x≤0,或x≥
| ||
D、{x|x<0,或x>
|
设集合M={x∈Z|x2+2x≤0},N={x|x2-2x=0,x∈R},则M∩N=( )
| A、{0} |
| B、{0,2} |
| C、{-2,0} |
| D、{-2,0,2} |
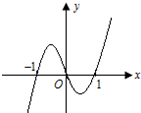 已知函数y=xf′(x)的图象如图所示(其中f′(x)是函数f(x)的导函数),则以下说法错误的是( )
已知函数y=xf′(x)的图象如图所示(其中f′(x)是函数f(x)的导函数),则以下说法错误的是( )| A、f′(1)+f′(-1)=0 |
| B、当x=-1时,函数f(x)取得极大值 |
| C、方程xf'(x)=0与f(x)=0均有三个实数根 |
| D、当x=1时,函数f(x)取得极小值 |