题目内容
已知椭圆E：
+
=1（a＞b＞0）的离心率e=
，并且经过定点P（
，
）．
（Ⅰ）求椭圆E的方程；
（Ⅱ）问是否存在直线y=-x+m，使直线与椭圆交于A、B两点，满足
•
=
，若存在求m值，若不存在说明理由．
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
| 3 |
| 1 |
| 2 |
（Ⅰ）求椭圆E的方程；
（Ⅱ）问是否存在直线y=-x+m，使直线与椭圆交于A、B两点，满足
| OA |
| OB |
| 12 |
| 5 |
考点：直线与圆锥曲线的综合问题
专题：圆锥曲线中的最值与范围问题
分析：（Ⅰ）由已知条件推导出e=
=
且
+
=1，由此能求出椭圆E的方程．
（Ⅱ）设A（x1，y1），B（x2，y2），由
•
=
得，x1x2+y1y2=
，联立方程组利用根与系数的关系求解即可得出m的值．
| c |
| a |
| ||
| 2 |
| 3 |
| a2 |
| 1 |
| 4b2 |
（Ⅱ）设A（x1，y1），B（x2，y2），由
| OA |
| OB |
| 12 |
| 5 |
| 12 |
| 5 |
解答：
解（Ⅰ）由题意：e=
=
且
+
=1，又c2=a2-b2
解得：a2=4，b2=1，即：椭圆E的方程为
+y2=1（1）
（Ⅱ）设A（x1，y1），B（x2，y2）
⇒x2+4(m-x)2-4=0⇒5x2-8mx+4m2-4=0（*）
所以x1+x2=
，x1x2=
y1y2=(m-x1)(m-x2)=m2-m(x1+x2)+x1x2=m2-
m2+
=
由
•
=
，
得(x1，y1)•(x2，y2)=
，x1x2+y1y2=
，
+
=
，m=±2
又方程（*）要有两个不等实根，△=(-8m)2-4×5(4m2-4)＞0，-
＜m＜
所以m=±2．
| c |
| a |
| ||
| 2 |
| 3 |
| a2 |
| 1 |
| 4b2 |
解得：a2=4，b2=1，即：椭圆E的方程为
| x2 |
| 4 |
（Ⅱ）设A（x1，y1），B（x2，y2）
|
所以x1+x2=
| 8m |
| 5 |
| 4m2-4 |
| 5 |
y1y2=(m-x1)(m-x2)=m2-m(x1+x2)+x1x2=m2-
| 8 |
| 5 |
| 4m2-4 |
| 5 |
| m2-4 |
| 5 |
由
| OA |
| OB |
| 12 |
| 5 |
得(x1，y1)•(x2，y2)=
| 12 |
| 5 |
| 12 |
| 5 |
| 4m2-4 |
| 5 |
| m2-4 |
| 5 |
| 12 |
| 5 |
又方程（*）要有两个不等实根，△=(-8m)2-4×5(4m2-4)＞0，-
| 5 |
| 5 |
所以m=±2．
点评：本题主要考查椭圆方程及性质的应用，考查学生直线与椭圆位置关系的判断及运算求解能力，注意运用根与系数的关系简化运算，属于中档题．
练习册系列答案
黄冈小状元解决问题天天练系列答案
相关题目
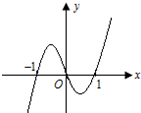已知函数y=xf′（x）的图象如图所示（其中f′（x）是函数f（x）的导函数），则以下说法错误的是（ ）| A、f′（1）+f′（-1）=0 |
| B、当x=-1时，函数f（x）取得极大值 |
| C、方程xf'（x）=0与f（x）=0均有三个实数根 |
| D、当x=1时，函数f（x）取得极小值 |
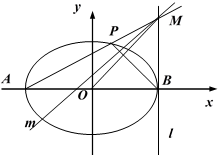（1）求椭圆E的方程；