设 m.n是两条不同的直线.α是一个平面.则下列命题正确的是( )A．若m∥n.n?α.则m∥αB．若m∥α.n?α.则m∥nC．若m⊥n.n?α.则m⊥αD．若m⊥α.m∥n.则n⊥α 题目和参考答案——青夏教育精英家教网—

题目内容

12．设 m、n是两条不同的直线，α是一个平面，则下列命题正确的是（　　）

A．

若m∥n，n?α，则m∥α

B．

若m∥α，n?α，则m∥n

C．

若m⊥n，n?α，则m⊥α

D．

若m⊥α，m∥n，则n⊥α

分析利用线面平行、垂直的性质与判定定理，即可得出结论．

解答解：线面平行的判定定理中要求直线m?α，所以A错误；
m∥α，n?α，则m∥n或m，n异面，所以错误；
根据线面垂直的判定定理，可知C不正确；
根据线面垂直的性质定理可知选项D正确．
故选：D．

点评本题主要考查空间直线和平面的位置关系的判断，要求熟练掌握相应的判定定理和性质定理．

练习册系列答案

3．设函数f（x）=$\frac{2}{3}$+$\frac{1}{x}$（x＞0），数列{a_n}满足a₁=1，a_n=f（$\frac{1}{{a}_{n-1}}$），n∈N^*，且n≥2．
（1）求数列{a_n}的通项公式；
（2）对n∈N^*，设S_n=$\frac{1}{a_1a_2}$+$\frac{1}{a_2a_3}$+$\frac{1}{a_3a_4}$+…+$\frac{1}{a_na_{n+1}}$，若S_n≥3t恒成立，求实数t的取值范围．

20．已知数列{a_n}的前n项和为S_n，满足a₁=2，S_n+2=2a_n，n∈N^*
（1）求a_n；
（2）求证：$\frac{a_1}{{（{{a_1}+1}）（{{a_2}+1}）}}+\frac{a_2}{{（{{a_2}+1}）（{{a_3}+1}）}}+…+\frac{a_n}{{（{{a_n}+1}）（{{a_{n+1}}+1}）}}＜\frac{1}{3}$．

7．若函数$f（x）=|sinx+\frac{2}{3+sinx}+t|（x，t∈R）$最大值记为g（t），则函数g（t）的最小值为$\frac{3}{4}$．

17．若椭圆C₁：$\frac{{x}^{2}}{{{a}_{1}}^{2}}$+$\frac{{y}^{2}}{{{b}_{1}}^{2}}$=1（a₁＞b₁＞0）和椭圆C₂：$\frac{{x}^{2}}{{{a}_{2}}^{2}}$+$\frac{{y}^{2}}{{{b}_{2}}^{2}}$=1（a₂＞b₂＞0）的焦点相同，且a₁＞a₂，则下面结论正确的是（　　）
①椭圆C₁和椭圆C₂一定没有公共点 ②a₁²-a₂²=b₁²-b₂²
③$\frac{{a}_{1}}{{a}_{2}}$＞$\frac{{b}_{1}}{{b}_{2}}$ ④a₁-a₂＜b₁-b₂．

4．顶点在原点、坐标轴为对称轴的抛物线，过点（-1，2），则它的方程是（　　）

1．求下列函数的导数．
（1）$y=\frac{e^x}{x}$；
（2）y=（2x²-1）（3x+1）

2．

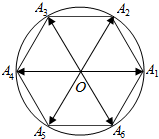已知正六边形A₁A₂…A₆内接于圆O，点P为圆O上一点，向量$\overrightarrow{OP}$与$\overrightarrow{O{A_i}}$的夹角为θ_i（i=1，2，…，6），若将θ₁，θ₂，…，θ₆从小到大重新排列后恰好组成等差数列，则该等差数列的第3项为$\frac{5π}{12}$．

试题分类