题目内容
解不等式:x(x-3)(2x+1)(x-1)(x3-1)≤0.
考点:其他不等式的解法
专题:不等式的解法及应用
分析:把原不等式等价转化为 x(2x+1)(x-3)(x-1)2≤0,再用穿根法求得它的解集.
解答:
解:x(x-3)(2x+1)(x-1)(x3-1)≤0,即 x(2x+1)(x-3)(x-1)2(x2+x+1)≤0.
由于x2+x+1>0,故不等式即 x(2x+1)(x-3)(x-1)2≤0,用穿根法求得它的解集为{x|x<-
0≤x≤3}.

由于x2+x+1>0,故不等式即 x(2x+1)(x-3)(x-1)2≤0,用穿根法求得它的解集为{x|x<-
| 1 |
| 2 |

点评:本题主要考查用穿根法解高次不等式,体现了转化、数形结合的数学思想,属于基础题.

练习册系列答案
相关题目
i是虚数单位,若复数z=
,则复数z的实部与虚部的和是( )
| 3+i |
| 1-i |
| A、3 | B、1+2i |
| C、2 | D、1-2i |
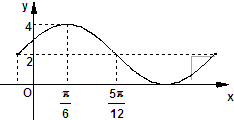 已知函数f(x)=Asin(ωx+ϕ)+B的一部分图象如图所示,如果A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+ϕ)+B的一部分图象如图所示,如果A>0,ω>0,|φ|<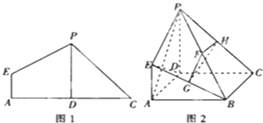 如图1,在平面四边形ACPE中,D为AC中点,AD=DC=PD=2,AE=1,且AE⊥AC,PD⊥AC,现沿PD折起使∠ADC=90°,得到立体图形(如图2),又B为平面ADC内一点,并且ABCD为正方形,设F,G,H分别为PB,EB,PC的中点.
如图1,在平面四边形ACPE中,D为AC中点,AD=DC=PD=2,AE=1,且AE⊥AC,PD⊥AC,现沿PD折起使∠ADC=90°,得到立体图形(如图2),又B为平面ADC内一点,并且ABCD为正方形,设F,G,H分别为PB,EB,PC的中点.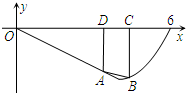 已知函数f(x)=
已知函数f(x)=