题目内容
已知函数f(x)=
的定义域为(-∞,1],求实数a的取值范围.
| 6x+4x+9xa |
考点:函数的定义域及其求法
专题:函数的性质及应用
分析:由题意6x+4x+9xa≥0在x∈(-∞,1]时恒成立,化为a≥-[(
)x+(
)x]在区间(-∞,1]上恒成立;
设t=(
)x+(
)x,求出t的最小值,即得a的取值范围.
| 2 |
| 3 |
| 4 |
| 9 |
设t=(
| 2 |
| 3 |
| 4 |
| 9 |
解答:
解:根据题意,6x+4x+9xa≥0在x∈(-∞,1]时恒成立,
即a≥-[(
)x+(
)x]在区间(-∞,1]上恒成立;
∴函数t=(
)x+(
)x=(
)2x+(
)x=((
)x+
)2-
,
在x=1时,t=
+
=
,
∴t≥
;
∴-t≤-
,
∴a≥-
;
即a的取值范围是[-
,+∞).
即a≥-[(
| 2 |
| 3 |
| 4 |
| 9 |
∴函数t=(
| 2 |
| 3 |
| 4 |
| 9 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 1 |
| 2 |
| 1 |
| 4 |
在x=1时,t=
| 2 |
| 3 |
| 4 |
| 9 |
| 10 |
| 9 |
∴t≥
| 10 |
| 9 |
∴-t≤-
| 10 |
| 9 |
∴a≥-
| 10 |
| 9 |
即a的取值范围是[-
| 10 |
| 9 |
点评:本题考查了求函数定义域的问题,解题时应用转化思想,化为求函数在某一区间上的最值问题,是易错题.

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案
相关题目
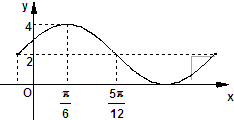 已知函数f(x)=Asin(ωx+ϕ)+B的一部分图象如图所示,如果A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+ϕ)+B的一部分图象如图所示,如果A>0,ω>0,|φ|<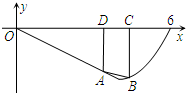 已知函数f(x)=
已知函数f(x)= 为了加强对H7N9的防控,某养鸭场要围成相同面积的长方形鸭笼四间(无盖),如图所示,一面可利用原有的墙,其他各面用铁丝网围成.
为了加强对H7N9的防控,某养鸭场要围成相同面积的长方形鸭笼四间(无盖),如图所示,一面可利用原有的墙,其他各面用铁丝网围成.