题目内容
已知椭圆C1:
+
=1(a>b>0)的左、右焦点分别为F1,F2,其中F2也是抛物线C2:y2=2px(p>0)的焦点,M(
,m)是C1与C2在第一象限内的交点,且|MF2|=
.
(1)求p的值与椭圆的方程;
(2)设点Q是椭圆上除长轴两端外的任意一点,试问在x轴上是否存在两定点A,B,使得直线QA,QB的斜率之积为定值?若存在,请求出定值以及定点A,B的坐标;若不存在,请说明理由.
| x2 |
| a2 |
| y2 |
| b2 |
| 2 |
| 3 |
| 5 |
| 3 |
(1)求p的值与椭圆的方程;
(2)设点Q是椭圆上除长轴两端外的任意一点,试问在x轴上是否存在两定点A,B,使得直线QA,QB的斜率之积为定值?若存在,请求出定值以及定点A,B的坐标;若不存在,请说明理由.
考点:直线与圆锥曲线的综合问题
专题:综合题,圆锥曲线的定义、性质与方程
分析:(1)利用点M(
,m)在抛物线上,且|MF2|=
,抛物线准线为x=-
,可得
+
=
,求出p,求得M的坐标,由它在椭圆上及椭圆右焦点为F2(1,0),求出a,b,即可求出椭圆的方程;
(2)求出直线QA,QB的斜率之积,利用直线QA,QB的斜率之积为定值,根据恒等关系,即可求出定点A,B的坐标.
| 2 |
| 3 |
| 5 |
| 3 |
| p |
| 2 |
| 2 |
| 3 |
| p |
| 2 |
| 5 |
| 3 |
(2)求出直线QA,QB的斜率之积,利用直线QA,QB的斜率之积为定值,根据恒等关系,即可求出定点A,B的坐标.
解答:
解:(1)因为点M(
,m)在抛物线上,且|MF2|=
,抛物线准线为x=-
,
所以,
+
=
,解得:p=2,…(3分)
所以,抛物线方程为y2=4x,焦点F2(1,0),
点M(
,m)代入y2=4x得m=
,所以点M(
,
),
由它在椭圆上及椭圆右焦点为F2(1,0)得
,解得
,
所以,椭圆方程为
+
=1.…(6分)
(2)设A(s,0)
B(t,0)
Q(x0,y0),因为点Q是椭圆上除长轴两端外的任意一点,
所以,
+
=
,即
=3(1-
),设直线QA,QB的斜率之积为定值k,…(8分)
所以,KQA•KQB=
•
=
=
=k,
所以,3-
=k
-k(s+t)x0+kst,所以,
⇒
o
,
所以,斜率之积为定值-
,定点A,B的坐标为(2,0),(-2,0).…(12分)
| 2 |
| 3 |
| 5 |
| 3 |
| p |
| 2 |
所以,
| 2 |
| 3 |
| p |
| 2 |
| 5 |
| 3 |
所以,抛物线方程为y2=4x,焦点F2(1,0),
点M(
| 2 |
| 3 |
2
| ||
| 3 |
| 2 |
| 3 |
2
| ||
| 3 |
由它在椭圆上及椭圆右焦点为F2(1,0)得
|
|
所以,椭圆方程为
| x2 |
| 4 |
| y2 |
| 3 |
(2)设A(s,0)
| , |
| , |
所以,
| x02 |
| 4 |
| y02 |
| 3 |
| 1 |
| y | 2 0 |
| ||
| 4 |
所以,KQA•KQB=
| y0 |
| x0-s |
| y0 |
| x0-t |
| ||
|
3(1-
| ||||
|
所以,3-
3
| ||
| 4 |
| x | 2 0 |
|
|
| r |
|
所以,斜率之积为定值-
| 3 |
| 4 |
点评:本题考查椭圆方程和求法和定点A,B的求法,解题时要认真审题,注意抛物线的性质的灵活运用,注意合理地进行等价转化.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
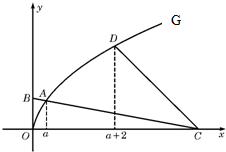 如图,曲线G的方程为y=
如图,曲线G的方程为y=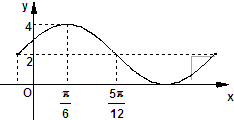 已知函数f(x)=Asin(ωx+ϕ)+B的一部分图象如图所示,如果A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+ϕ)+B的一部分图象如图所示,如果A>0,ω>0,|φ|<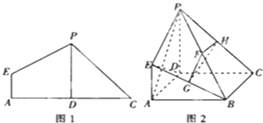 如图1,在平面四边形ACPE中,D为AC中点,AD=DC=PD=2,AE=1,且AE⊥AC,PD⊥AC,现沿PD折起使∠ADC=90°,得到立体图形(如图2),又B为平面ADC内一点,并且ABCD为正方形,设F,G,H分别为PB,EB,PC的中点.
如图1,在平面四边形ACPE中,D为AC中点,AD=DC=PD=2,AE=1,且AE⊥AC,PD⊥AC,现沿PD折起使∠ADC=90°,得到立体图形(如图2),又B为平面ADC内一点,并且ABCD为正方形,设F,G,H分别为PB,EB,PC的中点.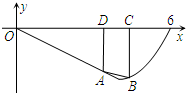 已知函数f(x)=
已知函数f(x)= 为了加强对H7N9的防控,某养鸭场要围成相同面积的长方形鸭笼四间(无盖),如图所示,一面可利用原有的墙,其他各面用铁丝网围成.
为了加强对H7N9的防控,某养鸭场要围成相同面积的长方形鸭笼四间(无盖),如图所示,一面可利用原有的墙,其他各面用铁丝网围成.