题目内容
15．已知{an}是等差数列，a2+a4+a98+a99=20，则前100项的和S100等于（ ）| A． | 500 | B． | 250 | C． | 50 | D． | 1000 |
分析 利用等差数列通项公式先求出a1+a100=10，由此能求出前100项的和S100．
解答 解：∵{an}是等差数列，a2+a4+a98+a99=20，
∴a2+a4+a98+a99=2（a1+a100）=20，
∴a1+a100=10，
∴前100项的和S100=$\frac{100}{2}（{a}_{1}+{a}_{100}）$=50×10=500．
故选为：A．
点评 本题考查等差数列的前100项和的求法，是基础题，解题时要认真审题，注意等差数列的性质的合理运用．
练习册系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
5．（x3-$\frac{2}{x}$）4的展开式中的常数项为（ ）
| A． | 32 | B． | 64 | C． | -32 | D． | -64 |
6．在平面四边形ABCD中，∠A=∠B=60°，∠C=75°，BC=2，则AB的取值范围是（ ）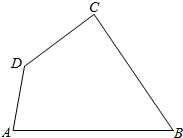
| A． | （$\sqrt{3}$-1，2） | B． | （2，$\sqrt{3}$+1） | C． | （$\sqrt{3}$-1，$\sqrt{3}$+1） | D． | （2，4） |
7．若a，b∈（0，1），则函数f（x）=x2-2ax+b在R上没零点的概率为（ ）
| A． | $\frac{1}{4}$ | B． | $\frac{1}{3}$ | C． | $\frac{1}{2}$ | D． | $\frac{2}{3}$ |