题目内容
1.函数f(x)=log3x+x-5的一个零点所在的区间为( )| A. | (0,1) | B. | (1,2) | C. | (2,3) | D. | (3,4) |
分析 确定函数的定义域为(0,+∞)与单调性,再利用零点存在定理,即可得到结论.
解答 解:函数的定义域为(0,+∞),易知函数在(0,+∞)上单调递增,
∵f(4)=log34+4-5>0,f(3)=log33+3-5<0,
∴函数f(x)=log3x+x-5的零点一定在区间(3,4),
故选:D.
点评 本题考查函数的单调性,考查零点存在定理,属于基础题.

练习册系列答案
相关题目
12.在生产过程中,测得纤维产品的纤度(表示纤维粗细的一种量)共有100个数据,将数据分组如表:
(1)画出频率分布直方图;
(2)估计纤度落在[1.38,1.50)中的频率及纤度小于1.40的频率是多少?
(3)从频率分布直方图估计出纤度的众数、中位数和平均数.
| 分组 | 频数 |
| [1.30,1.34) | 4 |
| [1.34,1.38) | 22 |
| [1.38,1.42) | 40 |
| [1.42,1.46) | 22 |
| [1.46,1.50) | 10 |
| [1.50,1.54) | 2 |
| 合计 | 100 |
(2)估计纤度落在[1.38,1.50)中的频率及纤度小于1.40的频率是多少?
(3)从频率分布直方图估计出纤度的众数、中位数和平均数.
16.如图,点(x,y)在阴影部分所表示的平面区域上,则z=y-x的最大值为( )
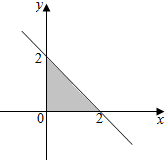

| A. | -2 | B. | 0 | C. | 1 | D. | 2 |
6.设△ABC的内角A,B,C所对的边分别为a,b,c,若acosB+bcosA=csinC,则△ABC的形状为( )
| A. | 锐角三角形 | B. | 等腰直角三角形 | C. | 钝角三角形 | D. | 直角三角形 |