题目内容
5.已知x>0,y>0且lg(x2+y2-4)≤0,则|2x+y-10|的取值范围是[5,8).分析 由题意可得点(x,y)表示圆环在第一象限的部分(如图阴影),令t=2x+y-10,则y=-2x+t+10,即t+10表示直线的截距,数形结合可得.
解答 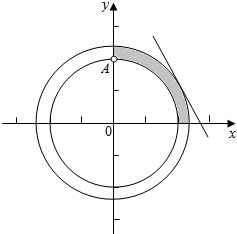 解:∵x>0,y>0且lg(x2+y2-4)≤0,
解:∵x>0,y>0且lg(x2+y2-4)≤0,
∴0<x2+y2-4≤1,即4<x2+y2≤5(x>0,y>0),
故点(x,y)表示圆环在第一象限的部分(如图阴影),
令t=2x+y-10,则y=-2x+t+10,即t+10表示直线的截距,
数形结合可得当直线y=-2x经过点A(0,2)时t+10取最小值2,此时t=-8,
当直线y=-2x与圆x2+y2=5相切时t+10取最大值5,此时t=-5,
故t的取值范围为(-8,-5],故|2x+y-10|的取值范围为[5,8),
故答案为:[5,8).
点评 本题考查式子的取值范围,数形结合是解决问题的关键,属中档题.

练习册系列答案
相关题目
13.已知数列{an}满足an>1,过点(an,0)的直线ln与圆x2+y2=1在第一象限相切于点Pn,若记Pn的横坐标为bn,则$\frac{{a}_{1}{b}_{1}+{a}_{2}{b}_{2}+..+{a}_{n}{b}_{n}}{({a}_{1}{a}_{2}…{a}_{n})({b}_{1}{b}_{2}…{b}_{n})}$等于( )
| A. | 2-21-n | B. | 2n-1 | C. | 1 | D. | n |
3.若a=30.5,b=logπ3,c=log30.5,则( )
| A. | a>b>c | B. | b>a>c | C. | c>a>b | D. | b>c>a |
1.函数f(x)=log3x+x-5的一个零点所在的区间为( )
| A. | (0,1) | B. | (1,2) | C. | (2,3) | D. | (3,4) |