题目内容
(1)判断函数f(x)=x3+
的奇偶性;
(2)判断函数f(x)=
在(-1,1)内的单调性并用单调性的定义证明.
| 1 |
| x3 |
(2)判断函数f(x)=
| x |
| x2-1 |
考点:函数奇偶性的判断,函数单调性的判断与证明
专题:函数的性质及应用
分析:(1)利用函数奇偶性的定义即可判断函数f(x)=x3+
的奇偶性;
(2)根据函数单调性的定义进行证明即可.
| 1 |
| x3 |
(2)根据函数单调性的定义进行证明即可.
解答:
解:(1)函数的定义域为(-∞,0)∪(0,+∞),
则f(-x)=-x3-
=-(x3+
)=-f(x),
故函数f(x)是奇函数;
(2)函数f(x)=
在(-1,1)内的单调递减,
设1>x1>x2>-1,
则f(x1)-f(x2)=
-
=
,
∵1>x1>x2>-1,
∴x2-x1>0,且x12<1,x22<1,x1x2<1,
∴f(x1)-f(x2)<0,即f(x1)<f(x2),
故函数f(x)在区间(-1,1)上是减函数.
则f(-x)=-x3-
| 1 |
| x3 |
| 1 |
| x3 |
故函数f(x)是奇函数;
(2)函数f(x)=
| x |
| x2-1 |
设1>x1>x2>-1,
则f(x1)-f(x2)=
| x1 |
| x12-1 |
| x2 |
| x22-1 |
| (x2-x1)(1+x1x2) |
| (x12-1)(x22-1) |
∵1>x1>x2>-1,
∴x2-x1>0,且x12<1,x22<1,x1x2<1,
∴f(x1)-f(x2)<0,即f(x1)<f(x2),
故函数f(x)在区间(-1,1)上是减函数.
点评:本题主要考查函数奇偶性和单调性的判断,根据奇偶性和单调性的定义是解决本题的关键.

练习册系列答案
相关题目
已知{an}为等比数列,Sn是它的前n项和.若a2•a3=2a1,且a4与2a7的等差中项为
,则S5=( )
| 5 |
| 4 |
| A、31 | B、32 | C、33 | D、34 |
如图,在同一直角坐标系中,正确表示直线y=ax与y=x+a的是( )
A、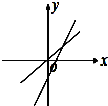 |
B、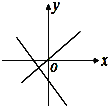 |
C、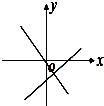 |
D、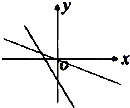 |
“m<1”是“函数f(x)=x2+x+m有零点”的( )
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
设a=log
6,b=(
)0.2,c=5
,则( )
| 1 |
| 5 |
| 1 |
| 6 |
| 1 |
| 6 |
| A、a<b<c |
| B、c<b<a |
| C、c<a<b |
| D、b<a<c |
下列各式中正确的是( )
A、sin2
| ||||||
B、若a∈(0,2π),则一定有tana=
| ||||||
C、sin
| ||||||
D、sina=tana•cosa(a≠kπ+
|