题目内容
已知{an}为等比数列，Sn是它的前n项和．若a2•a3=2a1，且a4与2a7的等差中项为
，则S5=（ ）
| 5 |
| 4 |
| A、31 | B、32 | C、33 | D、34 |
考点：等比数列的通项公式
专题：等差数列与等比数列
分析：设等比数列{an}的公比为q，由已知可得q和a1的值，代入等比数列的求和公式可得．
解答：
解：设等比数列{an}的公比为q，
则可得a1q•a1q2=2a1，即a4=a1q3=2，
又a4与2a7的等差中项为
，
所以a4+2a7=
，即2+2×2q3=
，
解得q=
，可得a1=16，
故S5=
=31．
故选：A．
则可得a1q•a1q2=2a1，即a4=a1q3=2，
又a4与2a7的等差中项为
| 5 |
| 4 |
所以a4+2a7=
| 5 |
| 2 |
| 5 |
| 2 |
解得q=
| 1 |
| 2 |
故S5=
16(1-
| ||
1-
|
故选：A．
点评：本题考查等比数列的通项公式和求和公式，涉及等差数列的性质，属基础题．
练习册系列答案
互动英语系列答案
相关题目
已知m，n是两条不重合的直线，α，β，γ是三个两两不重合的平面，给出下列四个命题
①若m⊥α，m⊥β，则α∥β；
②若α⊥β，β⊥γ，则α∥β；
③若m?a，n?β，m∥n，则α∥β；
④若m，n是异面直线，n?α，m∥β，n?β，n∥α，则α∥β．
其中真命题是（ ）
①若m⊥α，m⊥β，则α∥β；
②若α⊥β，β⊥γ，则α∥β；
③若m?a，n?β，m∥n，则α∥β；
④若m，n是异面直线，n?α，m∥β，n?β，n∥α，则α∥β．
其中真命题是（ ）
| A、①和② | B、①和③ |
| C、①和④ | D、③和④ |
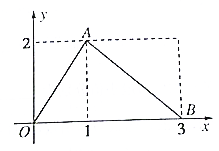函数y=f（x）的图象是如图所示的折线段OAB，已知点A坐标为（1，2）点B的坐标为（3，0），若P（x，y）是函数g（x）=f（x）（x-1）图象上的动点，则x+y的最大值为（ ）A、
| ||
| B、2 | ||
C、
| ||
| D、4 |
若等比数列{an}的前3项和等于首项的3倍，则该等比数列的公比为（ ）
| A、1 | B、-2 |
| C、2或-1 | D、-2或1 |
将函数y=sin（2x+
）图象上的所有点向左平移
个单位，得到的图象的函数解析式是（ ）
| π |
| 4 |
| π |
| 4 |
A、y=sin（2x+
| ||
B、y=sin（2x+
| ||
C、y=sin（2x-
| ||
| D、y=sin2x |