题目内容

解方程：
1-x
+
x+12
=5．
考点：根式与分数指数幂的互化及其化简运算
专题：计算题
分析：先求出x的取值范围，通过平方去掉根号，化为一元二次方程，解出即可．
解答： 解：∵1-x≥0，x+12≥0，
∴-12≤x≤1，
∵
1-x
+
x+12
=5，
∴1-x+x+12+2
(1-x)(x+12)
=25，
∴
(1-x)(x+12)
=6，
∴x2+11x+24=0，
解得：x=-3，x=-8．
点评：本题考查了解方程问题，考查了转化思想，是一道基础题．
练习册系列答案
相关题目
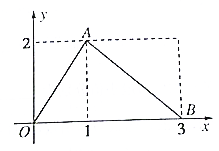函数y=f（x）的图象是如图所示的折线段OAB，已知点A坐标为（1，2）点B的坐标为（3，0），若P（x，y）是函数g（x）=f（x）（x-1）图象上的动点，则x+y的最大值为（　　）
A、
13
4
B、2
C、
7
4
D、4
设{an}是等差数列，Sn是其前n项和，若S2≤3，S3≥6，则S4的最小值为
 
．
若sinx-sin（
3π
2
-x）=
2
，则tanx+
1
tan(x-π)
的值是（　　）
A、2B、-1C、1D、2
在直角坐标系xOy中，O为坐标原点，点M的横纵坐标分别为茎叶图中位数和众数，若点N（x，y）的坐标满足
x2+y2≤4
2x-y≥0
y≥0
，求
OM
•
ON
的最大值．
有下列四个结论：
①函数f（x）=lg（x+1）+lg（x-1）的定义域是（1，+∞）
②若幂函数y=f（x）的图象经过点（2，4），则该函数为偶函数
③函数y=5|x|的值域是（0，+∞）
④函数f（x）=x+2x在（-1，0）有且只有一个零点．
其中正确结论的个数为（　　）
A、1B、2C、3D、4
（1）判断函数f（x）=x3+
1
x3
的奇偶性；
（2）判断函数f（x）=
x
x2-1
在（-1，1）内的单调性并用单调性的定义证明．
点（1，2）到直线y=2x+1的距离为（　　）
A、
5
5
B、
2
5
5
C、
5
D、2
5
已知直线a∥平面α，则下列命题是假命题的是（　　）
A、a与α内的无数条直线平行
B、a与α内的所有直线都平行
C、a与α内的无数条直线垂直
D、a与α无公共点

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网