题目内容
3.盒中装有7个零件,其中5个是没有使用过的,2个是使用过的.(Ⅰ)从盒中每次随机抽取1个零件,有放回的抽取3次,求3次抽取中恰有2次抽到使用过零件的概率;
(Ⅱ)从盒中任意抽取3个零件,使用后放回盒子中,设X为盒子中使用过零件的个数,求X的分布列和期望.
分析 (Ⅰ)记“从盒中随机抽取一个零件,抽到的是使用过零件”为事件A.可得P(A)=$\frac{{∁}_{2}^{1}}{{∁}_{7}^{1}}$.利用二项分布列可得:三次抽取中恰有2次抽到使用过零件的概率P=${∁}_{3}^{2}(\frac{2}{7})^{2}(\frac{5}{7})$.
(II)利用二项分布列的计算公式即可得出.
解答 解:(Ⅰ)记“从盒中随机抽取一个零件,抽到的是使用过零件”为事件A.
则P(A)=$\frac{{∁}_{2}^{1}}{{∁}_{7}^{1}}$=$\frac{2}{7}$.
所以三次抽取中恰有2次抽到使用过零件的概率P=${∁}_{3}^{2}(\frac{2}{7})^{2}(\frac{5}{7})$=$\frac{60}{343}$.
(Ⅱ)从盒中任意抽取三个零件,使用后放回盒子中,设此时盒子中使用过的零件个数为X,
由已知X=3,4,5.
P(X=3)=$\frac{{∁}_{5}^{1}{∁}_{2}^{2}}{{∁}_{7}^{3}}$=$\frac{1}{7}$,P(X=4)=$\frac{{∁}_{5}^{2}{∁}_{2}^{1}}{{∁}_{7}^{3}}$=$\frac{4}{7}$,P(X=5)=$\frac{{∁}_{5}^{3}}{{∁}_{7}^{3}}$=$\frac{2}{7}$.
随机变量X的分布列为:
| X | 3 | 4 | 5 |
| P | $\frac{1}{7}$ | $\frac{4}{7}$ | $\frac{2}{7}$ |
点评 本题考查了二项分布列与超几何分布列的概率计算公式及其数学期望,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
17.已知抛物线y2=6x,定点A(2,3),F为焦点,P为抛物线上的动点,则|PF|+|PA|的最小值为( )
| A. | 5 | B. | 4.5 | C. | 3.5 | D. | 不能确定 |
12.对标有不同编号的形状大小完全一样的5件正品和3件次品进行检测,现不放回地依次取出2件,则在第一次取出正品的条件下,第二次也取出正品的概率是( )
| A. | $\frac{1}{8}$ | B. | $\frac{5}{8}$ | C. | $\frac{5}{14}$ | D. | $\frac{4}{7}$ |
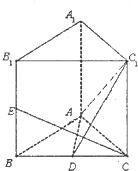 如图在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AB=AC=2$\sqrt{2}$,BC=BB1=4,D、E分别为BC,BB1的中点.
如图在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AB=AC=2$\sqrt{2}$,BC=BB1=4,D、E分别为BC,BB1的中点.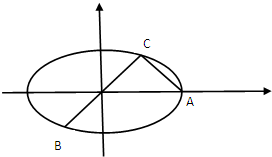 如图,已知A,B,C是长轴为4的椭圆E上的三点,点A是长轴的
如图,已知A,B,C是长轴为4的椭圆E上的三点,点A是长轴的