题目内容
14.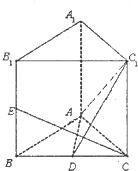 如图在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AB=AC=2$\sqrt{2}$,BC=BB1=4,D、E分别为BC,BB1的中点.
如图在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AB=AC=2$\sqrt{2}$,BC=BB1=4,D、E分别为BC,BB1的中点.(Ⅰ)求证:CE⊥平面AC1D;
(Ⅱ)求直线AB与平面AC1D所成角的正弦值.
分析 (Ⅰ)由已知可得,四边形CBB1C1为正方形,又D、E分别为BC,BB1的中点,得CE⊥C1D,再由已知可得AD⊥CE,结合线面垂直的判定得答案;
(Ⅱ)由D是BC的中点,可得B,C到平面AC1D的距离相等,由(Ⅰ)知,CE⊥平面AC1D,由射影定理可得C到平面AC1D的距离,从而得到B到平面AC1D的距离,而AB=2$\sqrt{2}$.可得直线AB与平面AC1D所成角的正弦值.
解答 (Ⅰ)证明:由已知可得,四边形CBB1C1为正方形,又D、E分别为BC,BB1的中点,
∴CE⊥C1D,
∵AB=AC,D为BC中点,∴AD⊥BC,则AD⊥平面CBB1C1,则AD⊥CE.
又C1D∩AD=D,∴CE⊥平面AC1D;
(Ⅱ)解:∵D是BC的中点,∴B,C到平面AC1D的距离相等,
由(Ⅰ)知,CE⊥平面AC1D,设垂足为M,在Rt△C1CD中,由射影定理可得$CM=\frac{4\sqrt{5}}{5}$,
∴B到平面AC1D的距离为$\frac{4\sqrt{5}}{5}$,而AB=2$\sqrt{2}$.
∴直线AB与平面AC1D所成角的正弦值为$\frac{\frac{4\sqrt{5}}{5}}{2\sqrt{2}}=\frac{\sqrt{10}}{5}$.
点评 本题考查直线与平面垂直的判定,考查了线面角的求法,考查空间想象能力和思维能力,是中档题.

练习册系列答案
相关题目
8.已知函数f(x)=$\left\{\begin{array}{l}{(1-x)^{3},x<1}\\{(x-1)^{3},x≥1}\end{array}\right.$,若关于x的不等式f(x2-2x+2)<f(1-a2x2)的解集中有且仅有三个整数,则实数a的取值范围是( )
| A. | [-$\frac{3}{4}$,-$\frac{2}{3}$)∪($\frac{2}{3}$,$\frac{3}{4}$] | B. | ($\frac{2}{3}$,$\frac{3}{4}$] | C. | [-$\frac{3}{4}$,-$\frac{1}{2}$)∪($\frac{1}{2}$,$\frac{3}{4}$] | D. | [-$\frac{4}{5}$,-$\frac{3}{4}$)∪($\frac{3}{4}$,$\frac{4}{5}$] |
9.设全集U={x∈R|x>0},函数f(x)=$\sqrt{1-lnx}$的定义域为A,则∁UA为( )
| A. | (e,+∞) | B. | [e,+∞) | C. | (0,e) | D. | (0,e] |
19.某中学为了解初三年级学生“掷实心球”项目的整体情况,随机抽取男、女生各20名进行测试,记录的数据如下:
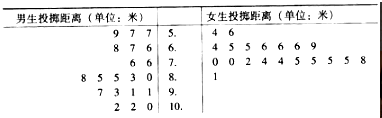
已知该项目评分标准为:
注:满分10分,且得9分以上(含9分)定为“优秀”.
(Ⅰ)求上述20名女生得分的中位数和众数;
(Ⅱ)从上述20名男生中,随机抽取2名,求抽取的2名男生中优秀人数X的分布列;
(Ⅲ)根据以上样本数据和你所学的统计知识,试估计该年级学生实心球项目的整体情况.(写出两个结论即可)

已知该项目评分标准为:
| 男生投掷距离(米) | … | [5.4,6.0) | [6.0,6.6) | [6.6,7.4) | [7.4,7.8) | [7.8,8.6) | [8.6,10.0) | [10.0,+∞) |
| 女生投掷距离(米) | … | [5.1,5.4) | [5.4,5.6) | [5.6,6.4) | [6.4,6.8) | [6.8,7.2) | [7.2,7.6) | [7.6,+∞) |
| 个人得分(分) | … | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
(Ⅰ)求上述20名女生得分的中位数和众数;
(Ⅱ)从上述20名男生中,随机抽取2名,求抽取的2名男生中优秀人数X的分布列;
(Ⅲ)根据以上样本数据和你所学的统计知识,试估计该年级学生实心球项目的整体情况.(写出两个结论即可)
6.设随机变量X的概率分布表如下:
若E(X)=2.5,则a-b的值为0.
| X | 1 | 2 | 3 | 4 |
| P | $\frac{1}{4}$ | a | $\frac{3}{8}$ | b |
4.已知某正方体的外接球的表面积是16π,则这个正方体的棱长是( )
| A. | $\frac{{2\sqrt{2}}}{3}$ | B. | $\frac{{2\sqrt{3}}}{3}$ | C. | $\frac{{4\sqrt{2}}}{3}$ | D. | $\frac{{4\sqrt{3}}}{3}$ |