题目内容
11.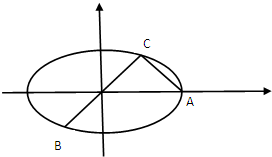 如图,已知A,B,C是长轴为4的椭圆E上的三点,点A是长轴的
如图,已知A,B,C是长轴为4的椭圆E上的三点,点A是长轴的一个端点,BC过椭圆中心O,且$\overrightarrow{AC}•\overrightarrow{BC}$=O,|BC|=2|AC|
(1)求椭圆E的方程.
(2)设圆O是以原点为圆心,短轴长为半径的园,过椭圆E上异于其顶点的任一点P,作圆O的两条切线,切点为M,N,若直线MN在x轴,Y轴上的截距分别为m,n,试计算$\frac{1}{{3{m^2}}}+\frac{1}{n^2}$的值是否为定值?如果,请给予证明;如果不是,请说明理由.
分析 (1)由已知得a,数形结合求得C的坐标,代入椭圆方程求得b,则椭圆方程可求;
(2)设P(x0,y0),由M,N是切点,可知P、M、O、N四点共圆.分别写出以PO为直径的圆的方程与圆O的方程,联立可得MN所在直线方程求出直线MN在x,y轴上的截距,结合P在椭圆上可得$\frac{1}{{3{m^2}}}+\frac{1}{n^2}$的值是定值.
解答 解:(1)由已知可得,a=2,设椭圆方程为$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{{b}^{2}}=1$.
由已知可得:|OB|=|OC|,又$\overrightarrow{AC}•\overrightarrow{BC}$=0,|BC|=|2AC|,
∴C(1,1),把C代入椭圆方程可得:$\frac{1}{4}+\frac{1}{{b}^{2}}=1$,得${b}^{2}=\frac{4}{3}$,
∴椭圆方程为:$\frac{{x}^{2}}{4}+\frac{3{y}^{2}}{4}=1$;
(2)设P(x0,y0),由M,N是切点,可知P、M、O、N四点共圆.
∴以PO为直径的圆的方程为:(x-x0)x+(y-y0)y=0,即x2+y2-x0x-y0y=0,①
又圆O的方程为:${x}^{2}+{y}^{2}=\frac{4}{3}$,②
联立①②可得MN所在直线方程为:${x}_{0}x+{y}_{0}y=\frac{4}{3}$.
直线MN在x,y轴上的截距分别为:$m=\frac{4}{3{x}_{0}},n=\frac{4}{3{y}_{0}}$.
∴$\frac{1}{{3{m^2}}}+\frac{1}{n^2}$=$\frac{3{{x}_{0}}^{2}+9{{y}_{0}}^{2}}{16}=\frac{3({{x}_{0}}^{2}+3{{y}_{0}}^{2})}{16}$.
又P(x0,y0)在椭圆上,∴$\frac{{{x}_{0}}^{2}}{4}+\frac{3{{y}_{0}}^{2}}{4}=1$,即${{x}_{0}}^{2}+3{{y}_{0}}^{2}=4$.
∴$\frac{1}{{3{m^2}}}+\frac{1}{n^2}$=$\frac{3×4}{16}=\frac{3}{4}$.
∴$\frac{1}{{3{m^2}}}+\frac{1}{n^2}$的值是定值.
点评 本题考查椭圆的简单性质,考查了直线与圆、圆与椭圆位置关系的应用,是中档题.

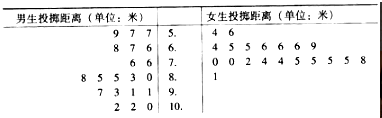
已知该项目评分标准为:
| 男生投掷距离(米) | … | [5.4,6.0) | [6.0,6.6) | [6.6,7.4) | [7.4,7.8) | [7.8,8.6) | [8.6,10.0) | [10.0,+∞) |
| 女生投掷距离(米) | … | [5.1,5.4) | [5.4,5.6) | [5.6,6.4) | [6.4,6.8) | [6.8,7.2) | [7.2,7.6) | [7.6,+∞) |
| 个人得分(分) | … | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
(Ⅰ)求上述20名女生得分的中位数和众数;
(Ⅱ)从上述20名男生中,随机抽取2名,求抽取的2名男生中优秀人数X的分布列;
(Ⅲ)根据以上样本数据和你所学的统计知识,试估计该年级学生实心球项目的整体情况.(写出两个结论即可)
| X | 1 | 2 | 3 | 4 |
| P | $\frac{1}{4}$ | a | $\frac{3}{8}$ | b |

| A. | 4410 | B. | 4010 | C. | 4020 | D. | 4400 |