题目内容
8.用数学归纳法证明“2n>n2,对于n≥n0的正整数n均成立”时,第一步证明中的起始值n0的最小值为( )| A. | 1 | B. | 3 | C. | 5 | D. | 7 |
分析 根据数学归纳法的步骤,验证n=1,2,3,4,5时,命题是否成立,可得答案.
解答 解:解:根据数学归纳法的步骤,首先要验证当n取第一个值时命题成立;
结合本题,要验证n=1时,左=21=2,右=12=1,2n>n2成立,
n=2时,左=22=4,右=22=4,2n>n2不成立,
n=3时,左=23=8,右=32=9,2n>n2不成立,
n=4时,左=24=16,右=42=16,2n>n2不成立,
n=5时,左=25=32,右=52=25,2n>n2成立,
因为n>5成立,所以2n>n2恒成立.
故第一步证明中的起始值n0的最小值为5,
故选C
点评 本题考查数学归纳法的运用,解此类问题时,注意n的取值范围,很容易做错.

练习册系列答案
相关题目
2.下列说法的正确的是( )
| A. | 经过定点P0(x0,y0)的直线都可以用方程y-y0=k(x-x0)表示 | |
| B. | 经过定点A(0,b)的直线都可以用方程y=kx+b表示 | |
| C. | 不经过原点的直线都可以用方程$\frac{x}{a}$+$\frac{y}{b}$=1表示P1(x1,y1)、P2(x2,y2) | |
| D. | 经过任意两个不同的点的直线都可以用方程(y-y1)(x2-x1)=(x-x1)(y2-y1)来表示 |
19.某中学为了解初三年级学生“掷实心球”项目的整体情况,随机抽取男、女生各20名进行测试,记录的数据如下:
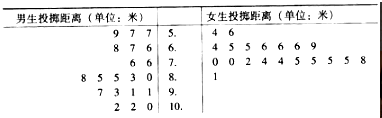
已知该项目评分标准为:
注:满分10分,且得9分以上(含9分)定为“优秀”.
(Ⅰ)求上述20名女生得分的中位数和众数;
(Ⅱ)从上述20名男生中,随机抽取2名,求抽取的2名男生中优秀人数X的分布列;
(Ⅲ)根据以上样本数据和你所学的统计知识,试估计该年级学生实心球项目的整体情况.(写出两个结论即可)

已知该项目评分标准为:
| 男生投掷距离(米) | … | [5.4,6.0) | [6.0,6.6) | [6.6,7.4) | [7.4,7.8) | [7.8,8.6) | [8.6,10.0) | [10.0,+∞) |
| 女生投掷距离(米) | … | [5.1,5.4) | [5.4,5.6) | [5.6,6.4) | [6.4,6.8) | [6.8,7.2) | [7.2,7.6) | [7.6,+∞) |
| 个人得分(分) | … | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
(Ⅰ)求上述20名女生得分的中位数和众数;
(Ⅱ)从上述20名男生中,随机抽取2名,求抽取的2名男生中优秀人数X的分布列;
(Ⅲ)根据以上样本数据和你所学的统计知识,试估计该年级学生实心球项目的整体情况.(写出两个结论即可)
13.已知正三棱锥P-ABC中E,F分别是AC,PC的中点,若EF⊥BF,AB=2,则三棱锥P-ABC的外接球的表面积( )
| A. | 4π | B. | 6π | C. | 8π | D. | 12π |