题目内容
已知函数f(x)=2x+
.
(1)判断函数y=f(x)的奇偶性;
(2)分别指出函数f(x)在区间(0,2)和(-2,0)上的单调性并证明;
(3)分别指出函数f(x)在区间(2,4)和(-4,-2)上的单调性并证明;
(4)由此你发现了什么结论?
| 1 |
| 2x |
(1)判断函数y=f(x)的奇偶性;
(2)分别指出函数f(x)在区间(0,2)和(-2,0)上的单调性并证明;
(3)分别指出函数f(x)在区间(2,4)和(-4,-2)上的单调性并证明;
(4)由此你发现了什么结论?
考点:函数单调性的判断与证明,函数奇偶性的判断
专题:函数的性质及应用,导数的综合应用
分析:(1)先求函数f(x)的定义域,根据奇函数的定义即可判断f(x)的奇偶性;
(2)求f′(x),根据f′(x)符号即可判断函数在(0,2),(-2,0)上的单调性;
(3)根据(2)求得的导数,判断导数在区间(2,4),(-4,-2)上的符号,即可判断函数在这两个区间上的单调性;
(4)通过观察函数f(x)在对称区间上的单调性,发现奇函数在对称区间上的单调性一致.
(2)求f′(x),根据f′(x)符号即可判断函数在(0,2),(-2,0)上的单调性;
(3)根据(2)求得的导数,判断导数在区间(2,4),(-4,-2)上的符号,即可判断函数在这两个区间上的单调性;
(4)通过观察函数f(x)在对称区间上的单调性,发现奇函数在对称区间上的单调性一致.
解答:
解:(1)函数f(x)的定义域是{x|x≠0};
f(-x)=-2x-
=-f(x),∴该函数为奇函数;
(2)f′(x)=2-
=
;
∴x∈(-2,-
)时,f′(x)>0;x∈(-
,0)时,f′(x)<0;x∈(0,
)时,f′(x)<0;x∈(
,2)时,f′(x)>0;
∴函数f(x)在(-
,0),(0,
)上单调递减,在(-2,-
],[
,2)上单调递增;
(3)由(2)知,x∈(2,4),x∈(-4,-2)时,f′(x)>0;
∴f(x)在(2,4),(-4,-2)上单调递增;
(4)得出的结论是:奇函数在对称区间上的单调性一样.
f(-x)=-2x-
| 1 |
| 2x |
(2)f′(x)=2-
| 1 |
| 2x2 |
4(x2-
| ||
| 2x2 |
∴x∈(-2,-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴函数f(x)在(-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(3)由(2)知,x∈(2,4),x∈(-4,-2)时,f′(x)>0;
∴f(x)在(2,4),(-4,-2)上单调递增;
(4)得出的结论是:奇函数在对称区间上的单调性一样.
点评:考查奇函数的定义,及判断方法,根据导数符号判断函数的单调性,以及奇函数在对称区间上的单调性的特点.

练习册系列答案
相关题目
下列区间中,一定存在函数f(x)=x3+3x-3的零点的是( )
| A、(-1,0) |
| B、(0,1) |
| C、(1,2) |
| D、(2,3) |
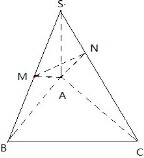 在三棱锥S-ABC中,SA⊥底面ABC,∠ABC=90°,且SA=AB,点M是SB的中点,AN⊥SC且交SC于点N.
在三棱锥S-ABC中,SA⊥底面ABC,∠ABC=90°,且SA=AB,点M是SB的中点,AN⊥SC且交SC于点N.