题目内容
平面直角坐标系中，O为坐标原点，已知两点A（3，1），B（-1，3），若点C满足
=α
+β
，其中α，β∈R且α+β=1，求点C的轨迹及其轨迹方程．
| OC |
| OA |
| OB |
考点：轨迹方程,平面向量的基本定理及其意义
专题：计算题,直线与圆
分析：通过点C满足
=α
+β
，其中α、β∈R，且α+β=1，知点C在直线AB上，利用两点式方程，求出直线AB的方程即求出点C的轨迹方程．
| OC |
| OA |
| OB |
解答：
解：C点满足
=α
+β
，且α+β=1，由共线向量定理可知，A、B、C三点共线．
∴C点的轨迹是直线AB
又A（3，1）、B（-1，3），
∴直线AB的方程为：
=
整理得x+2y-5=0
故C点的轨迹方程为x+2y-5=0．
| OC |
| OA |
| OB |
∴C点的轨迹是直线AB
又A（3，1）、B（-1，3），
∴直线AB的方程为：
| y-1 |
| 3-1 |
| x-3 |
| -1-3 |
故C点的轨迹方程为x+2y-5=0．
点评：考查平面向量中三点共线的充要条件及知两点求直线的方程，是向量与解析几何综合运用的一道比较基本的题，难度较小，知识性较强．
练习册系列答案
习题精选系列答案
相关题目
有三个球，一个球内切于正方体的各个面，另一个球切正方体的各条棱，第三个球过正方体的各个顶点（都是同一正方体），则这三个球的体积之比为（ ）
A、1：
| ||||
| B、1：2：3 | ||||
C、1：2
| ||||
| D、1：4：3 |
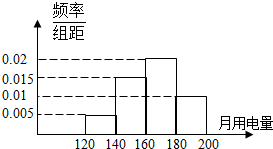
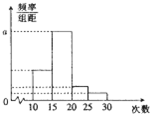对某校高一年级学生参加社区服务次数统计，随机抽取M名学生作为样本，得到这M名学生参加社区服务的次数．根据此数据作出了频数与频率的统计表和频率分布直方图如下：