题目内容
在四棱锥P-ABCD中，若PA⊥平面ABCD，且四边形ABCD是菱形，求证：平面PAC⊥平面PBD．
考点：平面与平面垂直的判定
专题：空间位置关系与距离
分析：首先，连结AC和BD，则AC⊥BD，然后，利用PA⊥平面ABCD，BD⊥平面PAC即可．
解答：
解：如图示，连结AC和BD，相交于点O，
∵四边形ABCD是菱形，
∴AC⊥BD，
∵PA⊥平面ABCD，
∴PA⊥BD，且PA∩AC=A，
∴BD⊥平面PAC，
∴平面PAC⊥平面PBD．
∵四边形ABCD是菱形，
∴AC⊥BD，
∵PA⊥平面ABCD，
∴PA⊥BD，且PA∩AC=A，
∴BD⊥平面PAC，
∴平面PAC⊥平面PBD．
点评：本题重点考查了空间中垂直关系，线面垂直和线线垂直，面面垂直等知识，属于中档题．
练习册系列答案
名校课堂系列答案
相关题目
从10名班委中选出两名担任班长和副班长；有（ ）种不同选法．
A、
| ||
B、
| ||
C、
| ||
| D、2 |
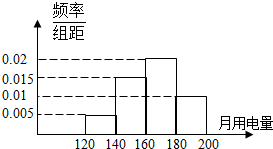
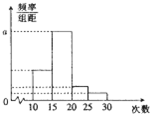对某校高一年级学生参加社区服务次数统计，随机抽取M名学生作为样本，得到这M名学生参加社区服务的次数．根据此数据作出了频数与频率的统计表和频率分布直方图如下：