Question

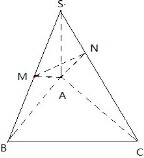在三棱锥S-ABC中，SA⊥底面ABC，∠ABC=90°，且SA=AB，点M是SB的中点，AN⊥SC且交SC于点N．
（1）求证：SC⊥平面AMN；
（2）当AB=BC=1时，求三棱锥M-SAN的体积．

Answer 1

考点：棱柱、棱锥、棱台的体积,空间中直线与直线之间的位置关系

专题：空间位置关系与距离

分析：（1）依题意，可证得CB⊥平面SAB，从而可证CB⊥AM；由SA=AB，点M是SB的中点可证得AM⊥SB，而CB∩SB=B，从而AM⊥平面SCB⇒AM⊥SC，进一步可证SC⊥平面AMN，利用面面垂直的判断定理即可证得结论．
（2）利用（1）的结果，通过数据关系，求出AM，MN，SN，然后求出棱锥的体积．

解答： 解：（1）证明：∵SA⊥平面ABC，
∴SA⊥CB
∵ABC直角三角形，
∴CB⊥AB，且SA∩AB=A，
∴CB⊥平面SAB，
∴CB⊥AM
∵SA=AB，M为SB的中点，
∴AM⊥SB，且CB∩SB=B，
∴AM⊥平面SCB，
∴AM⊥SC   
又∵SC⊥AN，且AN∩AM=A，
∴SC⊥平面AMN．
（2）由（1）可知∠AMN=∠SNM=∠SNA=90°，
∵SA=AB=BC=1，
∴AM=SM=MB=

2

2

，SC=

3

，MN=

BC•SM

SC

=

6

6

．SN=

SB•SM

SC

=

3

3

．
SC⊥平面AMN，
∴三棱锥M-SAN的体积：

1

3

×

1

2

×AM•MN•SN=

1

3

×

1

2

×

2

2

×

6

6

×

3

3

=

1

36

．

点评：本题重点考查了空间中直线与平面垂直，直线与直线垂直等位置关系，解题关键是线面垂直和线线垂直的相互转化，棱锥体积的求法，属于中档题．