题目内容
5.已知点M的直角坐标为 ( $\sqrt{3}$,-1)则它的极坐标可以是( )| A. | ( 2,$\frac{2π}{3}$ ) | B. | ( 2,$\frac{5π}{6}$ ) | C. | (2,$\frac{5π}{3}$) | D. | ( 2,$\frac{11π}{6}$ ) |
分析 利用直角坐标和极坐标互化公式直接求解.
解答 解:∵点M的直角坐标为 ( $\sqrt{3}$,-1),
∴$ρ=\sqrt{3+1}$=2,
tanθ=$\frac{-1}{\sqrt{3}}$=-$\frac{\sqrt{3}}{3}$,∴θ=$\frac{11π}{6}$,
∴点M的极坐标为M(2,$\frac{11π}{6}$).
故选:D.
点评 本题考查点的极坐标的求法,是基础题,解题时要认真审题,注意直角坐标和极坐标互化公式的合理运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
20.已知函数f(x)=x3-3x2+ax+2,曲线y=f(x)在点(0,2)处的切线与x轴交点的横坐标为-2,则a的值为( )
| A. | 1 | B. | 3 | C. | $\frac{1}{2}$ | D. | 5 |
10.已知点A是抛物线x2=4y的对称轴与准线的交点,点F为抛物线的焦点,P在抛物线上且满足|PA|=m|PF|,当m取最大值时|PA|的值为( )
| A. | 1 | B. | $\sqrt{5}$ | C. | $\sqrt{6}$ | D. | 2$\sqrt{2}$ |
17.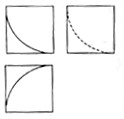 如图所示,某几何体的三视图是三个边长为1的正方形及每个正方形内一段半径为1,圆心角为90°的圆弧,则该几何体的体积是( )
如图所示,某几何体的三视图是三个边长为1的正方形及每个正方形内一段半径为1,圆心角为90°的圆弧,则该几何体的体积是( )
 如图所示,某几何体的三视图是三个边长为1的正方形及每个正方形内一段半径为1,圆心角为90°的圆弧,则该几何体的体积是( )
如图所示,某几何体的三视图是三个边长为1的正方形及每个正方形内一段半径为1,圆心角为90°的圆弧,则该几何体的体积是( )| A. | 1-$\frac{π}{12}$ | B. | 1-$\frac{π}{3}$ | C. | 1-$\frac{π}{6}$ | D. | 1-$\frac{π}{24}$ |
14.若变量x,y满足条件$\left\{\begin{array}{l}x-y-1≤0\\ x+y-6≤0\\ x-3≥0\end{array}\right.$,则xy的取值范围是( )
| A. | [0,5] | B. | $[{5,\frac{35}{4}}]$ | C. | $[{0,\frac{35}{4}}]$ | D. | [6,9] |