题目内容
10.已知点A是抛物线x2=4y的对称轴与准线的交点,点F为抛物线的焦点,P在抛物线上且满足|PA|=m|PF|,当m取最大值时|PA|的值为( )| A. | 1 | B. | $\sqrt{5}$ | C. | $\sqrt{6}$ | D. | 2$\sqrt{2}$ |
分析 过P作准线的垂线,垂足为N,则由抛物线的定义,结合|PA|=m|PF|,设PA的倾斜角为α,则当m取得最大值时,sinα最小,此时直线PA与抛物线相切,求出P的坐标,即可求得|PA|的值.
解答  解:抛物线的标准方程为x2=4y,
解:抛物线的标准方程为x2=4y,
则抛物线的焦点为F(0,1),准线方程为y=-1,
过P作准线的垂线,垂足为N,
则由抛物线的定义可得|PN|=|PF|,
∵|PA|=m|PF|,∴|PA|=m|PN|,
设PA的倾斜角为α,则sinα=$\frac{1}{m}$,
当m取得最大值时,sinα最小,此时直线PA与抛物线相切,
设直线PA的方程为y=kx-1,代入x2=4y,
可得x2=4(kx-1),
即x2-4kx+4=0,
∴△=16k2-16=0,∴k=±1,
∴P(2,1),
∴|PA|=$\sqrt{4+4}$=2$\sqrt{2}$.
故选D.
点评 本题考查抛物线的性质,考查抛物线的定义,考查学生分析解决问题的能力,解答此题的关键是明确当m取得最大值时,sinα最小,此时直线PA与抛物线相切,属中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.曲线C1的极坐标方程为ρ=R(R>0),曲线C2的参数方程为$\left\{\begin{array}{l}{x=2+si{n}^{2}α}\\{y=si{n}^{2}α}\end{array}\right.$(α为参数),若C1与C2有公共点,则R的取值范围是( )
| A. | [2,+∞) | B. | [$\sqrt{2}$,+∞) | C. | [2,$\sqrt{10}$] | D. | [2,3] |
5.已知点M的直角坐标为 ( $\sqrt{3}$,-1)则它的极坐标可以是( )
| A. | ( 2,$\frac{2π}{3}$ ) | B. | ( 2,$\frac{5π}{6}$ ) | C. | (2,$\frac{5π}{3}$) | D. | ( 2,$\frac{11π}{6}$ ) |
19.执行如图所示的程序框图,输出的y值为( )
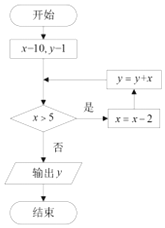

| A. | 15 | B. | 17 | C. | 19 | D. | 21 |
20.已知数列{an}是等差数列,若a2016+a2017<0,a2016•a2017<0,且数列{an}的前n项和Sn有最小值,那么Sn取得最小正值时,n等于( )
| A. | 4029 | B. | 4030 | C. | 4031 | D. | 4032 |