题目内容
17．
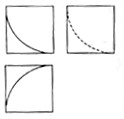如图所示，某几何体的三视图是三个边长为1的正方形及每个正方形内一段半径为1，圆心角为90°的圆弧，则该几何体的体积是（ ）| A． | 1-$\frac{π}{12}$ | B． | 1-$\frac{π}{3}$ | C． | 1-$\frac{π}{6}$ | D． | 1-$\frac{π}{24}$ |
分析 由三视图可知：该几何体为一个棱长为1的正方体去掉一个球的$\frac{1}{8}$，其中球心为正方体的一个顶点，半径为1．
1．
解答 解：由三视图可知：该几何体为一个棱长为1的正方体去掉一个球的$\frac{1}{8}$，
其中球心为正方体的一个顶点，半径为1．
∴该几何体的体积V=1-$\frac{1}{8}×\frac{4}{3}π×{1}^{3}$=1-$\frac{π}{6}$．
故选：C．
点评 本题考查了正方体与球的三视图、体积计算公式，考查了推理能力与计算能力，属于基础题．
练习册系列答案
相关题目
8．已知某产品的广告费用x与销售额y之间有如下的对应数据：
（1）y与x是否具有线性相关关系？若有，求出y对x的线性回归方程；
（2）据此估计广告费用为11万元时销售额的值．
（参考公式：$\stackrel{∧}{b}$=$\frac{{{\sum_{i=1}^{n}x}_{i}y}_{i}-n\overline{x}\overline{y}}{{\sum_{i=1}^{n}x}_{i}^{2}-{n\overline{x}}^{2}}$，$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$）
| x（万元） | 2 | 4 | 5 | 6 | 8 |
| y（万元） | 30 | 40 | 60 | 50 | 70 |
（2）据此估计广告费用为11万元时销售额的值．
（参考公式：$\stackrel{∧}{b}$=$\frac{{{\sum_{i=1}^{n}x}_{i}y}_{i}-n\overline{x}\overline{y}}{{\sum_{i=1}^{n}x}_{i}^{2}-{n\overline{x}}^{2}}$，$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$）
5．已知点M的直角坐标为 （ $\sqrt{3}$，-1）则它的极坐标可以是（ ）
| A． | （ 2，$\frac{2π}{3}$ ） | B． | （ 2，$\frac{5π}{6}$ ） | C． | （2，$\frac{5π}{3}$） | D． | （ 2，$\frac{11π}{6}$ ） |