题目内容
8.定义域为R的函数f(x)对任意x都有f(1+x)=f(1-x),且其导数f′(x)满足(x-1)f′(x)>0,则当2<m<4时,有( )| A. | f(2)>f(2m)>f(log2m) | B. | f(log2m)>f(2m)>f(2) | C. | f(2m)>f(log2m)>f(2) | D. | f(2m)>f(2)>f(log2m) |
分析 先根据条件求出函数的对称轴,再求出函数的单调区间,然后判定2、log2m、2m的大小关系,根据单调性比较f(2)、f(log2m)、f(2m)的大小即可.
解答 解:∵函数f(x)对任意x都有f(1+x)=f(1-x),
∴函数f(x)的对称轴为x=1,
∵导函数f′(x)满足(x-1)f′(x)>0,
∴函数f(x)在(1,+∞)上单调递增,(-∞,1)上单调递减,
∵2<m<4,
∴2m>4>2>log2m,
∴f(2m)>f(2)>f(log2m),
故选:D.
点评 本题主要考查了导数的运算,以及奇偶函数图象的对称性和比较大小,同时考查了数形结合的思想,该题有一定的思维量,属于基础题之列.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
18.中心在原点,焦点在x轴上,焦距等于12,离心率等于$\frac{3}{5}$,则此椭圆的方程是( )
| A. | $\frac{{x}^{2}}{100}$+$\frac{{y}^{2}}{36}$=1 | B. | $\frac{{x}^{2}}{100}$+$\frac{{y}^{2}}{64}$=1 | C. | $\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{16}$=1 | D. | $\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{9}$=1 |
19.已知定点M(-3,0),N(2,0),如果动点P满足|PM|=2|PN|,则点P的轨迹所包围的图形面积等于( )
| A. | $\frac{100π}{9}$ | B. | $\frac{142π}{9}$ | C. | $\frac{10π}{3}$ | D. | 9π |
16.在某化学反应的中间阶段,压力保持不变,温度从1°变化到5°,反应结果如下表所示(x代表温度,y代表结果):
(1)求化学反应的结果y对温度x的线性回归方程$\widehaty=\widehatbx+\widehata$;
(2)判断变量x与y之间是正相关还是负相关,并预测当温度达到10°时反应结果为多少?
| x | 1 | 2 | 3 | 4 | 5 |
| y | 3 | 5 | 7 | 10 | 11 |
(2)判断变量x与y之间是正相关还是负相关,并预测当温度达到10°时反应结果为多少?
13.某几何体三视图如图所示,则该几何体的表面积为( )
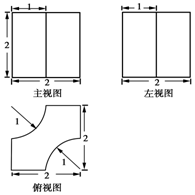

| A. | 8+2π | B. | 16+2π | C. | 20+2π | D. | 16+π |
17.若集合A={x|(x+2)(x-5)<0},集合B={x|-3<x<4},全集为R,则A∩B等于( )
| A. | [4,5) | B. | (-2,4) | C. | (-3,-2) | D. | (2,4) |
4.下列说法正确的是( )
①|$\sqrt{(x+4)^{2}+{y}^{2}}$|-|$\sqrt{(x-4)^{2}+{y}^{2}}$=0
②|$\sqrt{(x+4)^{2}+{y}^{2}}$+$\sqrt{(x-4)^{2}+{y}^{2}}$=14
③|$\sqrt{(x+4)^{2}+{y}^{2}}$-$\sqrt{(x-4)^{2}+{y}^{2}}$|=6
④|$\sqrt{(x+4)^{2}+{y}^{2}}$-$\sqrt{(x-4)^{2}+{y}^{2}}$|=18.
①|$\sqrt{(x+4)^{2}+{y}^{2}}$|-|$\sqrt{(x-4)^{2}+{y}^{2}}$=0
②|$\sqrt{(x+4)^{2}+{y}^{2}}$+$\sqrt{(x-4)^{2}+{y}^{2}}$=14
③|$\sqrt{(x+4)^{2}+{y}^{2}}$-$\sqrt{(x-4)^{2}+{y}^{2}}$|=6
④|$\sqrt{(x+4)^{2}+{y}^{2}}$-$\sqrt{(x-4)^{2}+{y}^{2}}$|=18.
| A. | ①表示无轨迹 ②的轨迹是射线 | B. | ②的轨迹是椭圆 ③的轨迹是双曲线 | ||
| C. | ①的轨迹是射线④的轨迹是直线 | D. | ②、④均表示无轨迹 |