题目内容
3.已知集合A={x|2≤2x≤8},B={x|x>2},全集U=R.(1)求(∁UB)∪A;
(2)已知集合C={x|1<x<a},若C⊆A,求实数a的取值范围.
分析 (1)化简A,即可求(∁UB)∪A;
(2)已知集合C={x|1<x<a},若C⊆A,分类讨论,求实数a的取值范围.
解答 解:(1)A={x|2≤2x≤8}={x|1≤x≤3},B={x|x>2},…(3分)
(CUB)∪A={x|x≤3} …(6分)
(2)①当a≤1时,C=∅,此时C⊆A; …(8分)
②当a>1时,C⊆A,则1<a≤3 …(10分)
综合①②,可得a的取值范围是(-∞,3].…(12分)
点评 本题考查集合的运算与关系,考查分类讨论的数学思想,考查学生的计算能力,属于中档题.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
13.下列函数没有零点的是( )
| A. | $f(x)={log_2}^x-3$ | B. | $f(x)=\sqrt{x}-4$ | C. | f(x)=$\frac{1}{x-1}$ | D. | f(x)=x2+2x |
14.双曲线$\frac{x^2}{16}-\frac{y^2}{8}=1$的虚轴长是( )
| A. | 2 | B. | $4\sqrt{2}$ | C. | $2\sqrt{2}$ | D. | 8 |
8.定义域为R的函数f(x)对任意x都有f(1+x)=f(1-x),且其导数f′(x)满足(x-1)f′(x)>0,则当2<m<4时,有( )
| A. | f(2)>f(2m)>f(log2m) | B. | f(log2m)>f(2m)>f(2) | C. | f(2m)>f(log2m)>f(2) | D. | f(2m)>f(2)>f(log2m) |
15.命题“若 $α=\frac{π}{4}$,则 tanα=1”的逆否命题是( )
| A. | 若 $α≠\frac{π}{4}$,则tanα≠1 | B. | 若 $α=\frac{π}{4}$,则tanα≠1 | ||
| C. | 若 tanα≠1,则$α≠\frac{π}{4}$ | D. | 若 tanα≠1,则$α=\frac{π}{4}$ |
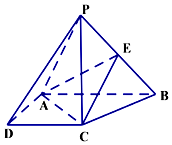 如图,在四棱锥P-ABCD中,PC⊥底面ABCD,ABCD是直角梯形,AB⊥AD,AB∥CD,AB=2AD=2CD=2,E是PB的中点.
如图,在四棱锥P-ABCD中,PC⊥底面ABCD,ABCD是直角梯形,AB⊥AD,AB∥CD,AB=2AD=2CD=2,E是PB的中点.