题目内容
18.中心在原点,焦点在x轴上,焦距等于12,离心率等于$\frac{3}{5}$,则此椭圆的方程是( )| A. | $\frac{{x}^{2}}{100}$+$\frac{{y}^{2}}{36}$=1 | B. | $\frac{{x}^{2}}{100}$+$\frac{{y}^{2}}{64}$=1 | C. | $\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{16}$=1 | D. | $\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{9}$=1 |
分析 根据题意,由题意可得2c=12.即c=6,结合椭圆的离心率计算公式e=$\frac{c}{a}$可得a=10,进而计算可得b2的值,将其代入椭圆的标准方程即可得答案.
解答 解:根据题意,此椭圆的焦点在x轴上,焦距等于12,
即2c=12,解可得c=6,
又由其离心率为e=$\frac{c}{a}$=$\frac{3}{5}$,
则a=10,b2=a2-c2=64;
则该椭圆的标准方程为$\frac{{x}^{2}}{100}$+$\frac{{y}^{2}}{64}$=1;
故选:B.
点评 本题考查椭圆的简单几何性质,关键是掌握离心率的计算公式,注意焦距为2c.

练习册系列答案
相关题目
9.若x,y满足$\left\{\begin{array}{l}x+y≤4\\ x-2y≥0\\ x+2y≥4\end{array}\right.$,则$z=\frac{y-4}{x-3}$的取值范围是( )
| A. | (-∞,-4]∪[3,+∞) | B. | (-∞,-2]∪[-1,+∞) | C. | [-2,-1] | D. | [-4,3] |
13.下列函数没有零点的是( )
| A. | $f(x)={log_2}^x-3$ | B. | $f(x)=\sqrt{x}-4$ | C. | f(x)=$\frac{1}{x-1}$ | D. | f(x)=x2+2x |
10.圆C:x2+y2-4=0被直线l:x-y+2=0截得的弦长为( )
| A. | $2\sqrt{3}$ | B. | $4\sqrt{3}$ | C. | $2\sqrt{2}$ | D. | $4\sqrt{2}$ |
8.定义域为R的函数f(x)对任意x都有f(1+x)=f(1-x),且其导数f′(x)满足(x-1)f′(x)>0,则当2<m<4时,有( )
| A. | f(2)>f(2m)>f(log2m) | B. | f(log2m)>f(2m)>f(2) | C. | f(2m)>f(log2m)>f(2) | D. | f(2m)>f(2)>f(log2m) |
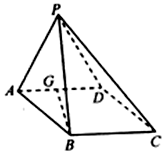 如图所示,在四棱锥P-ABCD中,G为AD的中点,侧面PAD⊥底面ABCD.底面ABCD是边长为a的菱形,且∠D A B=60°,侧面PAD为正三角形.求证:AD⊥平面PGB.
如图所示,在四棱锥P-ABCD中,G为AD的中点,侧面PAD⊥底面ABCD.底面ABCD是边长为a的菱形,且∠D A B=60°,侧面PAD为正三角形.求证:AD⊥平面PGB.