题目内容
8．函数f（x）=x2-alnx（a∈R）（a∈R）不存在极值点，则a的取值范围是（ ）| A． | （-∞，0） | B． | （0，+∞） | C． | [0，+∞） | D． | （-∞，0] |
分析 求出函数的导数，问题转化为a＜2x2在（0，+∞）恒成立，求出a的范围即可．
解答 解：f（x）的定义域是（0，+∞），
f′（x）=2x-$\frac{a}{x}$=$\frac{{2x}^{2}-a}{x}$，
若f（x）在（0，+∞）不存在极值点，
则a＜2x2在（0，+∞）恒成立，
故a≤0，
故选：D．
点评 本题考查了导数的应用，考查函数的单调性问题，是一道基础题．
练习册系列答案
习题精选系列答案
相关题目
18．若角α的终边经过点（1，-5），则tanα等于（ ）
| A． | -5 | B． | 5 | C． | -$\frac{1}{5}$ | D． | $\frac{1}{5}$ |
19．已知f（x）是R上的奇函数，当x≥0时，f（x）=$\left\{\begin{array}{l}{lo{g}_{2}（x+1），0≤x＜1}\\{|x-3|，x≥1}\end{array}\right.$，则函数y=f（x）-$\frac{1}{2}$的所有零点之和是（ ）
| A． | 5+$\sqrt{2}$ | B． | 1-$\sqrt{2}$ | C． | $\sqrt{2}$-1 | D． | 5-$\sqrt{2}$ |
16．在如图的程序框图中，若输入的x值为2，则输出的y值为（ ）
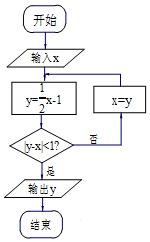
| A． | 0 | B． | $\frac{1}{2}$ | C． | -$\frac{3}{2}$ | D． | -1 |