Question

函数f（x）=Asin（ωx+φ）（A＞0，ω＞0）的部分图象如图所示，则f（x）的解析式可以为（　　）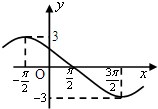

• A、f(x)=3sin(2x-

  π

  4

  )
• B、f(x)=3sin(2x+

  π

  4

  )
• C、f(x)=3sin(

  1

  2

  x-

  3π

  4

  )
• D、f(x)=3sin(

  1

  2

  x+

  3π

  4

  )

Answer 1

考点：由y=Asin（ωx+φ）的部分图象确定其解析式

专题：三角函数的图像与性质

分析：由图象观察可得：A=3，

1

2

T=

3π

2

+

π

2

，从而解得ω的值，又函数图象过点（-

π

2

，3），可解得φ的值，从而得解．

解答： 解：由题意可得：A=3，

1

2

T=

3π

2

+

π

2

，从而解得：T=4π，从而可求ω=

2π

T

=

2π

4π

=

1

2

∵函数图象过点（-

π

2

，3），
∴3=3sin（-

1

2

×

π

2

+φ），
∴可解得：φ=2kπ+

3π

4

，k∈Z
∴当k=0时有：φ=

3π

4

，
故选：D．

点评：本题主要考查了由y=Asin（ωx+φ）的部分图象确定其解析式，属于基本知识的考查．