题目内容
已知函数f(x)是(-∞,+∞)上的奇函数,若对于x≥0,都有f(x+2)=f(x),且当x∈[0,2)时,f(x)=log2(x+1),则f(-2015)+f(2014)的值为( )
| A、2 | B、1 | C、-1 | D、-2 |
考点:抽象函数及其应用,函数奇偶性的性质,对数的运算性质
专题:函数的性质及应用
分析:首先根据f(x)是(-∞,+∞)上的奇函数,可得f(-x)=-f(x),知f(-2015)=-f(2015),求出函数的周期T=2,利用当x∈[0,2)时,f(x)=log2(x+1)的解析式,进行求解.
解答:
解:∵函数f(x)是(-∞,+∞)上的奇函数,
∴f(-x)=-f(x),
又∵对于x≥0都有f(x+2)=f(x),
∴T=2,∵当x∈[0,2)时,f(x)=log2(x+1),
∴f(-2015)+f(2014)=-f(2015)+f(2014)=-f(2×1007+1)+f(2×1007)
=-f(1)+f(0)=-log22+log21=-1,
故选C.
∴f(-x)=-f(x),
又∵对于x≥0都有f(x+2)=f(x),
∴T=2,∵当x∈[0,2)时,f(x)=log2(x+1),
∴f(-2015)+f(2014)=-f(2015)+f(2014)=-f(2×1007+1)+f(2×1007)
=-f(1)+f(0)=-log22+log21=-1,
故选C.
点评:此题主要考查抽象函数的应用,函数的偶函数的性质及其周期性,还考查了周期函数的解析式,是一道基础题,计算的时候要仔细.

练习册系列答案
相关题目
已知正数a,b满足a+2b=1,则
+
的最小值为( )
| 2 |
| a |
| 3 |
| b |
| A、8 | ||
B、8+4
| ||
C、8+2
| ||
| D、20 |
a=20.3,b=0.32,c=log25,则a,b,c的大小关系为( )
| A、c<b<a |
| B、b<c<a |
| C、b<a<c |
| D、a<b<c |
函数f(x)=Asin(ωx+φ)(A>0,ω>0)的部分图象如图所示,则f(x)的解析式可以为( )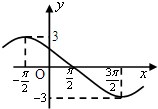

A、f(x)=3sin(2x-
| ||||
B、f(x)=3sin(2x+
| ||||
C、f(x)=3sin(
| ||||
D、f(x)=3sin(
|
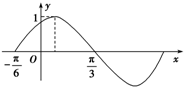 函数f(x)=sin(ωx+φ)(ω>0,|φ|<
函数f(x)=sin(ωx+φ)(ω>0,|φ|<