题目内容
已知f(x)=x3-3x,则函数h(x)=f[f(x)]的零点个数是( )
| A、3 | B、5 | C、7 | D、9 |
考点:函数零点的判定定理
专题:函数的性质及应用
分析:求出f(x)的导数,找出函数f(x)的根个数及分布区间,从而判断出函数h(x)的根的个数.
解答:
解:∵f′(x)=3x2-3=3(x+1)(x-1),
∴极值点为x=-1,1,
f(-1)=2为极大值,
f(1)=-2为极小值,
因此f(x)=0有3个不同的实根,
由f(-2)=-2<0,
f(2)=2>0,
知三个实根x1,x2,x3分别位于区间(-2,-1),(-1,1),(1,2),
h(x)的零点相当于
f(x)=x1,
f(x)=x2,
f(x)=x3,
同样由上分析,以上每个方程都有3个不同的实根,
所以h(x)共有9个不同的零点;
故选:D.
∴极值点为x=-1,1,
f(-1)=2为极大值,
f(1)=-2为极小值,
因此f(x)=0有3个不同的实根,
由f(-2)=-2<0,
f(2)=2>0,
知三个实根x1,x2,x3分别位于区间(-2,-1),(-1,1),(1,2),
h(x)的零点相当于
f(x)=x1,
f(x)=x2,
f(x)=x3,
同样由上分析,以上每个方程都有3个不同的实根,
所以h(x)共有9个不同的零点;
故选:D.
点评:本题考察了函数的零点问题,导数的应用问题,是一道中档题.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案
相关题目
下列各式的导数计算正确的是( )
A、(lgx)′=
| ||
B、(ln5)′=
| ||
| C、(x2sinx)′=2xcosx | ||
| D、(3x)′=3xln3 |
化简
的结果是( )
| 1-sin260° |
| A、cos60° |
| B、-cos60° |
| C、±cos60° |
| D、±|cos60°| |
将参加冬季越野跑的600名选手编号为:001,002,…,600.采用系统抽样方法抽取一个容量为50的样本,把编号分50组后,在第一组的001到012这12个编号中随机抽得的号码为004.这600名选手分别穿着三种颜色的衣服,从001到311穿红色衣服,从312到496穿白色衣服,从497到600穿黄色衣服.若从样本中任意抽取一个,则抽到穿白色衣服的选手的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
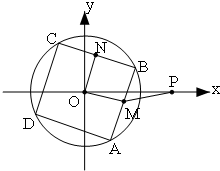 如图,已知点P(2,0),正方形ABCD内接于⊙O:x2+y2=2,M、N分别为边AB、BC的中点,当正方形ABCD绕圆心O旋转时,
如图,已知点P(2,0),正方形ABCD内接于⊙O:x2+y2=2,M、N分别为边AB、BC的中点,当正方形ABCD绕圆心O旋转时,| PM |
| ON |
| A、[-1,1] | ||||||||
B、[-
| ||||||||
| C、[-2,2] | ||||||||
D、[-
|
已知α=2,则点P(sinα,tanα)所在的象限是( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
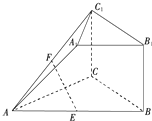 如图所示的几何体中,四边形BB1C1C是矩形,BB1⊥平面ABC,CA=CB,A1B1∥AB,AB=2A1B1,E,F分别是AB,AC1的中点.
如图所示的几何体中,四边形BB1C1C是矩形,BB1⊥平面ABC,CA=CB,A1B1∥AB,AB=2A1B1,E,F分别是AB,AC1的中点.