题目内容
已知
=(sina-cosa,2007),
=(sina+cosa,1),且
∥
,则tan2a-
=( )
| a |
| b |
| a |
| b |
| 1 |
| cos2a |
| A、-2007 | ||
B、-
| ||
| C、2007 | ||
D、
|
考点:三角函数的恒等变换及化简求值,平面向量共线(平行)的坐标表示
专题:计算题,三角函数的求值
分析:利用共线向量的坐标运算易求得
=2007,利用二倍角的余弦与正弦公式将所求关系式tan2a-
化简后代入,即可.
| sina-cosa |
| sina+cosa |
| 1 |
| cos2a |
解答:
解:∵
=(sina-cosa,2007),
=(sina+cosa,1),且
∥
,
∴(sina-cosa)×1-2007(sina+cosa)=0,
∴
=2007,
∴tan2a-
=
=-
=-
=
=2007.
故答案为:C.
| a |
| b |
| a |
| b |
∴(sina-cosa)×1-2007(sina+cosa)=0,
∴
| sina-cosa |
| sina+cosa |
∴tan2a-
| 1 |
| cos2a |
| sin2a-1 |
| cos2a |
| (cosa-sina)2 |
| cos2a-sin2a |
| cosa-sina |
| cosa+sina |
| sina-cosa |
| sina+cosa |
故答案为:C.
点评:本题考查平面向量共线(平行)的坐标运算,考查三角函数的恒等变换及化简求值,求得tana=-
是关键,属于中档题.
| 1004 |
| 1003 |

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
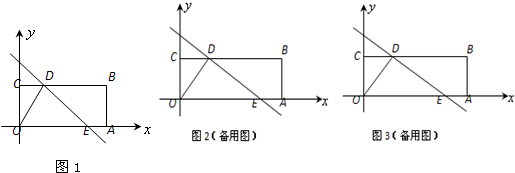
 如图,在三棱锥P-ABC中,BC⊥平面PAB.已知PA=AB,D,E分别为PB,BC的中点.
如图,在三棱锥P-ABC中,BC⊥平面PAB.已知PA=AB,D,E分别为PB,BC的中点.