题目内容
 如图,在三棱锥P-ABC中,BC⊥平面PAB.已知PA=AB,D,E分别为PB,BC的中点.
如图,在三棱锥P-ABC中,BC⊥平面PAB.已知PA=AB,D,E分别为PB,BC的中点.(1)求证:AD⊥平面PBC;
(2)若点F在线段AC上,且满足AD∥平面PEF,求
| AF |
| FC |
考点:直线与平面垂直的判定,直线与平面垂直的性质
专题:计算题,空间位置关系与距离
分析:(1)等腰△PAB中,证出中线AD⊥PB.由BC⊥平面PAB,得BC⊥AD,再利用线面垂直判定定理,即可证出AD⊥平面PBC;
(2)连结DC,交PE于点G,连结FG、DE.利用线面平行的性质定理,证出AD∥FG.而DE为△BPC的中位线,证出△DEG∽△CPG,利用相似三角形的性质和平行线的性质,即可算出
的值.
(2)连结DC,交PE于点G,连结FG、DE.利用线面平行的性质定理,证出AD∥FG.而DE为△BPC的中位线,证出△DEG∽△CPG,利用相似三角形的性质和平行线的性质,即可算出
| AF |
| FC |
解答:
解:(1)∵BC⊥平面PAB,AD?平面PAB,∴BC⊥AD.
∵PA=AB,D是PB的中点,∴AD⊥PB
∵PB、BC是平面PBC内的相交直线,∴AD平面PBC;
(2)连结DC,交PE于点G,连结FG、DE
∵AD∥平面PEF,AD?平面ADC,平面ADC∩平面PEF=FG,
∴AD∥FG.
∵D、E分别是PB、BC的中点,∴DE为△BPC的中位线,
因此,△DEG∽△CPG,可得
=
=
,
∴
=
=
,即
的值为
.

∵PA=AB,D是PB的中点,∴AD⊥PB
∵PB、BC是平面PBC内的相交直线,∴AD平面PBC;
(2)连结DC,交PE于点G,连结FG、DE
∵AD∥平面PEF,AD?平面ADC,平面ADC∩平面PEF=FG,
∴AD∥FG.
∵D、E分别是PB、BC的中点,∴DE为△BPC的中位线,
因此,△DEG∽△CPG,可得
| DG |
| GC |
| DE |
| PC |
| 1 |
| 2 |
∴
| AF |
| FC |
| DG |
| GC |
| 1 |
| 2 |
| AF |
| FC |
| 1 |
| 2 |
点评:本题在特殊的三棱锥中证明线面垂直,并求线段的比值.着重考查了线面垂直的定义与判定、线面平行性质定理和相似三角形的计算等知识,属于中档题.

练习册系列答案
相关题目
已知实数a,b满足(
)a>(
)b,则下列不等式一定成立的是( )
| 1 |
| 2 |
| 1 |
| 2 |
| A、a2>b2 |
| B、|a|<|b| |
| C、log2a<log2b |
| D、1-2a>1-2b |
已知
=(sina-cosa,2007),
=(sina+cosa,1),且
∥
,则tan2a-
=( )
| a |
| b |
| a |
| b |
| 1 |
| cos2a |
| A、-2007 | ||
B、-
| ||
| C、2007 | ||
D、
|
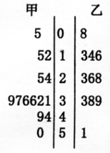 如图为甲、乙两名篮球运动员每场比赛的得分情况的茎叶图,则甲运动员的得分的中位数是
如图为甲、乙两名篮球运动员每场比赛的得分情况的茎叶图,则甲运动员的得分的中位数是 M、N是正方体ABCD-A1B1C1D1的棱A1B1、A1D1的中点,如图是用过M、N、A和D、N、C1的平面截去两个角后所得几何体,该几何体的主视图是( )
M、N是正方体ABCD-A1B1C1D1的棱A1B1、A1D1的中点,如图是用过M、N、A和D、N、C1的平面截去两个角后所得几何体,该几何体的主视图是( )


