题目内容
已知半径为5的圆的圆心C在x轴上,圆心C的横坐标是整数,且圆C与直线4x+3y-33=0相切.
(1)求圆C的方程;
(2)设直线ax-y-7=0与圆C相交于A,B两点,且满足CA⊥CB,求实数a的值.
(1)求圆C的方程;
(2)设直线ax-y-7=0与圆C相交于A,B两点,且满足CA⊥CB,求实数a的值.
考点:直线和圆的方程的应用
专题:计算题,直线与圆
分析:(1)利用圆C与直线4x+3y-33=0相切,结合圆心C的横坐标是整数,求出圆心的坐标,即可求圆C的方程;
(2)圆心C到直线ax-y-7=0为
,结合点到直线的距离公式,即可求实数a的值.
(2)圆心C到直线ax-y-7=0为
| 5 |
| 2 |
| 2 |
解答:
解:(1)设C(m,0),
∵圆C与直线4x+3y-33=0相切,∴
=5,
∴m=
或m=2,
∵圆心C的横坐标是整数,∴m=2,
∴圆C的方程为(x-2)2+y2=25.
(2)∵CA⊥CB且CA=CB=5,∴圆心C到直线ax-y-7=0为
,
∴
=
,化简得17a2+56a-73=0,
解得a=1或a=-
.
∵圆C与直线4x+3y-33=0相切,∴
| |4m-33| |
| 5 |
∴m=
| 29 |
| 2 |
∵圆心C的横坐标是整数,∴m=2,
∴圆C的方程为(x-2)2+y2=25.
(2)∵CA⊥CB且CA=CB=5,∴圆心C到直线ax-y-7=0为
| 5 |
| 2 |
| 2 |
∴
| |2a-7| | ||
|
| 5 |
| 2 |
| 2 |
解得a=1或a=-
| 73 |
| 17 |
点评:本题考查直线和圆的方程的应用,考查点到直线的距离公式,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
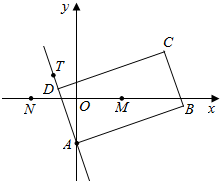 如图,矩形ABCD的两条对角线相交于点M(2,0),AB边所在直线的方程为
如图,矩形ABCD的两条对角线相交于点M(2,0),AB边所在直线的方程为