题目内容
 如图,矩形ABCD的两条对角线相交于点M(2,0),AB边所在直线的方程为
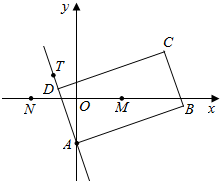
如图,矩形ABCD的两条对角线相交于点M(2,0),AB边所在直线的方程为x-3y-6=0,点T(-1,1)在AD边所在直线上.
(1)求AD边所在直线的方程;
(2)求矩形ABCD外接圆的方程;
(3)过点N(-2,0)的直线l与矩形ABCD的外接圆相交于P,Q两点,求
|
| NP |
| NQ |
考点:直线的一般式方程与直线的垂直关系
专题:直线与圆
分析:( I)由AD与AB垂直,求出直线AD的斜率,由此能求出AD边所在直线的方程.
( II)由
,解得点A(0,-2),因为矩形ABCD两条对角线的交点为M(2,0).所以M为矩形ABCD外接圆的圆心.由此能求出矩形ABCD外接圆的方程.
( III)过点N作圆的切线,切点为S,由此利用切割线定理能求出结果.
( II)由
|
( III)过点N作圆的切线,切点为S,由此利用切割线定理能求出结果.
解答:
 解:( I)因为AB边所在直线的方程为x-3y-6=0,且AD与AB垂直,
解:( I)因为AB边所在直线的方程为x-3y-6=0,且AD与AB垂直,
所以直线AD的斜率为-3.
又因为点T(-1,1)在直线AD上,
所以AD边所在直线的方程为y-1=-3(x+1),
即3x+y+2=0.
( II)由
,解得点A的坐标为(0,-2),
因为矩形ABCD两条对角线的交点为M(2,0).
所以M为矩形ABCD外接圆的圆心.
又|AM|=
=2
.
从而矩形ABCD外接圆的方程为(x-2)2+y2=8.
( III)过点N作圆的切线,切点为S,
则|
|•|
|=|
|2=|
|2-|
|2=8.
 解:( I)因为AB边所在直线的方程为x-3y-6=0,且AD与AB垂直,
解:( I)因为AB边所在直线的方程为x-3y-6=0,且AD与AB垂直,所以直线AD的斜率为-3.
又因为点T(-1,1)在直线AD上,
所以AD边所在直线的方程为y-1=-3(x+1),
即3x+y+2=0.
( II)由
|
因为矩形ABCD两条对角线的交点为M(2,0).
所以M为矩形ABCD外接圆的圆心.
又|AM|=
| (2-0)2+(0+2)2 |
| 2 |
从而矩形ABCD外接圆的方程为(x-2)2+y2=8.
( III)过点N作圆的切线,切点为S,
则|
| NP |
| NQ |
| NS |
| NM |
| MS |
点评:本题考查直线方程的求法,考查圆的方程的求法,考查向量数量积的求法,解题时要认真审题,注意直线性质的灵活运用.

练习册系列答案
相关题目
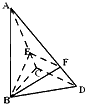 已知三棱锥A-BCD中,∠BCD=90°,BC=CD=1,AB⊥平面BCD,∠ADB=60°,E、F分别是AC、AD上的动点,且
已知三棱锥A-BCD中,∠BCD=90°,BC=CD=1,AB⊥平面BCD,∠ADB=60°,E、F分别是AC、AD上的动点,且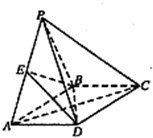 如图,四棱锥P-ABCD的底面ABCD是矩形,侧面PAB是正三角形,AB=2,
如图,四棱锥P-ABCD的底面ABCD是矩形,侧面PAB是正三角形,AB=2,